CoolMomentum: A Method for Stochastic Optimization by Langevin Dynamics with Simulated Annealing

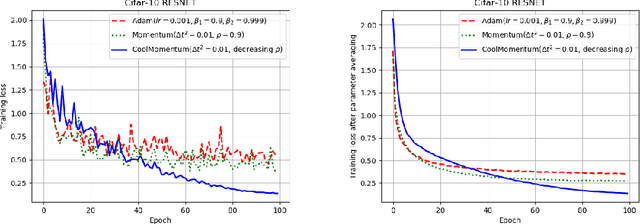
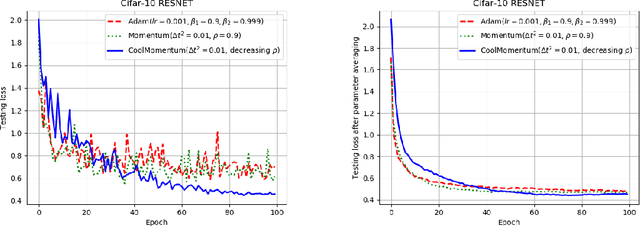
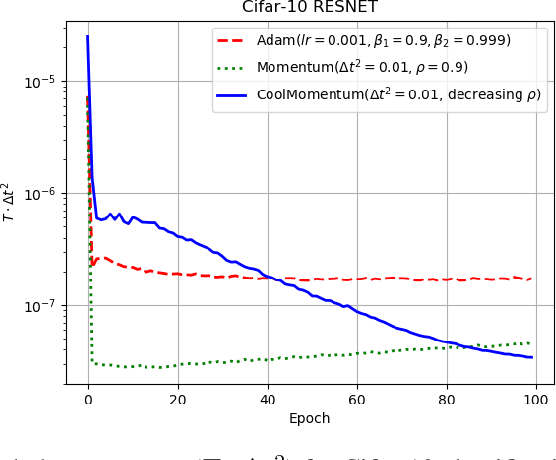
Deep learning applications require optimization of nonconvex objective functions. These functions have multiple local minima and their optimization is a challenging problem. Simulated Annealing is a well-established method for optimization of such functions, but its efficiency depends on the efficiency of the adapted sampling methods. We explore relations between the Langevin dynamics and stochastic optimization. By combining the Momentum optimizer with Simulated Annealing, we propose CoolMomentum - a prospective stochastic optimization method. Empirical results confirm the efficiency of the proposed theoretical approach.

A Simple Algorithm for Scalable Monte Carlo Inference

Statistical inference involves estimation of parameters of a model based on observations. Building on the recently proposed Equilibrium Expectation approach and Persistent Contrastive Divergence, we derive a simple and fast Markov chain Monte Carlo algorithm for maximum likelihood estimation (MLE) of parameters of exponential family distributions. The algorithm has good scaling properties and is suitable for Monte Carlo inference on large network data with billions of tie variables. The performance of the algorithm is demonstrated on Markov random fields, conditional random fields, exponential random graph models and Boltzmann machines.

Fast Maximum Likelihood estimation via Equilibrium Expectation for Large Network Data

A major line of contemporary research on complex networks is based on the development of statistical models that specify the local motifs associated with macro-structural properties observed in actual networks. This statistical approach becomes increasingly problematic as network size increases. In the context of current research on efficient estimation of models for large network data sets, we propose a fast algorithm for maximum likelihood estimation (MLE) that afords a signifcant increase in the size of networks amenable to direct empirical analysis. The algorithm we propose in this paper relies on properties of Markov chains at equilibrium, and for this reason it is called equilibrium expectation (EE). We demonstrate the performance of the EE algorithm in the context of exponential random graphmodels (ERGMs) a family of statistical models commonly used in empirical research based on network data observed at a single period in time. Thus far, the lack of efcient computational strategies has limited the empirical scope of ERGMs to relatively small networks with a few thousand nodes. The approach we propose allows a dramatic increase in the size of networks that may be analyzed using ERGMs. This is illustrated in an analysis of several biological networks and one social network with 104,103 nodes