CoolMomentum: A Method for Stochastic Optimization by Langevin Dynamics with Simulated Annealing
Paper and Code
May 29, 2020
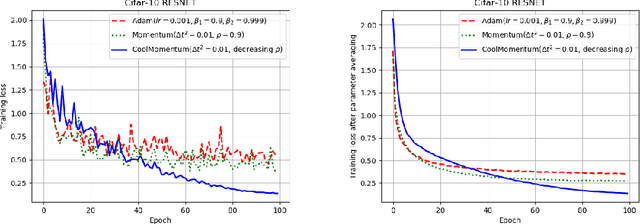
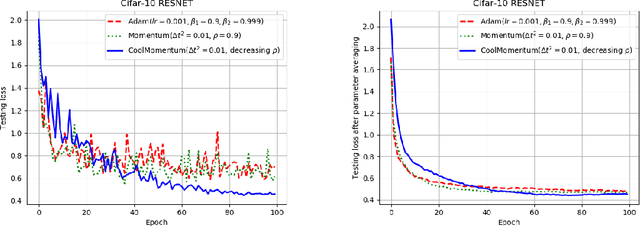
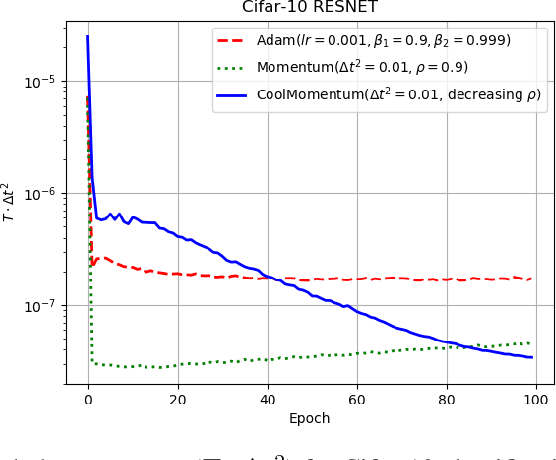
Deep learning applications require optimization of nonconvex objective functions. These functions have multiple local minima and their optimization is a challenging problem. Simulated Annealing is a well-established method for optimization of such functions, but its efficiency depends on the efficiency of the adapted sampling methods. We explore relations between the Langevin dynamics and stochastic optimization. By combining the Momentum optimizer with Simulated Annealing, we propose CoolMomentum - a prospective stochastic optimization method. Empirical results confirm the efficiency of the proposed theoretical approach.
* 9 pages, 6 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge