Application of Langevin Dynamics to Advance the Quantum Natural Gradient Optimization Algorithm

A Quantum Natural Gradient (QNG) algorithm for optimization of variational quantum circuits has been proposed recently. In this study, we employ the Langevin equation with a QNG stochastic force to demonstrate that its discrete-time solution gives a generalized form of the above-specified algorithm, which we call Momentum-QNG. Similar to other optimization algorithms with the momentum term, such as the Stochastic Gradient Descent with momentum, RMSProp with momentum and Adam, Momentum-QNG is more effective to escape local minima and plateaus in the variational parameter space and, therefore, achieves a better convergence behavior compared to the basic QNG. Our open-source code is available at https://github.com/borbysh/Momentum-QNG

CoolMomentum: A Method for Stochastic Optimization by Langevin Dynamics with Simulated Annealing

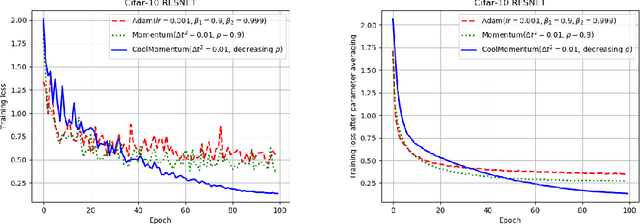
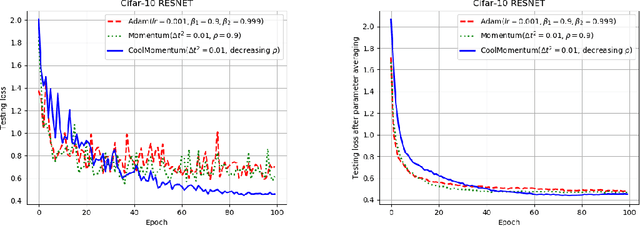
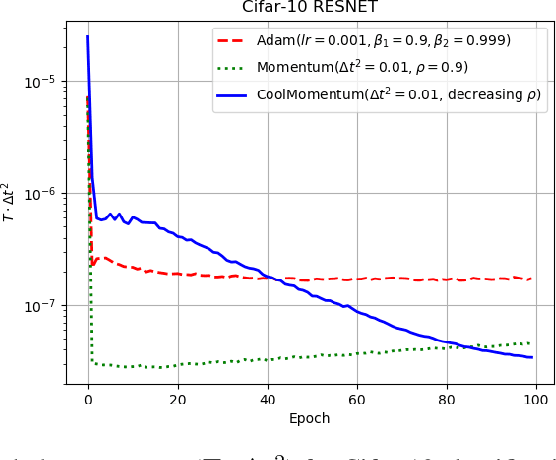
Deep learning applications require optimization of nonconvex objective functions. These functions have multiple local minima and their optimization is a challenging problem. Simulated Annealing is a well-established method for optimization of such functions, but its efficiency depends on the efficiency of the adapted sampling methods. We explore relations between the Langevin dynamics and stochastic optimization. By combining the Momentum optimizer with Simulated Annealing, we propose CoolMomentum - a prospective stochastic optimization method. Empirical results confirm the efficiency of the proposed theoretical approach.