Black-box optimization and quantum annealing for filtering out mislabeled training instances

This study proposes an approach for removing mislabeled instances from contaminated training datasets by combining surrogate model-based black-box optimization (BBO) with postprocessing and quantum annealing. Mislabeled training instances, a common issue in real-world datasets, often degrade model generalization, necessitating robust and efficient noise-removal strategies. The proposed method evaluates filtered training subsets based on validation loss, iteratively refines loss estimates through surrogate model-based BBO with postprocessing, and leverages quantum annealing to efficiently sample diverse training subsets with low validation error. Experiments on a noisy majority bit task demonstrate the method's ability to prioritize the removal of high-risk mislabeled instances. Integrating D-Wave's clique sampler running on a physical quantum annealer achieves faster optimization and higher-quality training subsets compared to OpenJij's simulated quantum annealing sampler or Neal's simulated annealing sampler, offering a scalable framework for enhancing dataset quality. This work highlights the effectiveness of the proposed method for supervised learning tasks, with future directions including its application to unsupervised learning, real-world datasets, and large-scale implementations.

Learning dynamic Boltzmann machines with spike-timing dependent plasticity

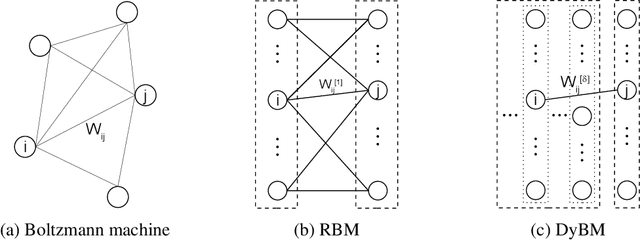
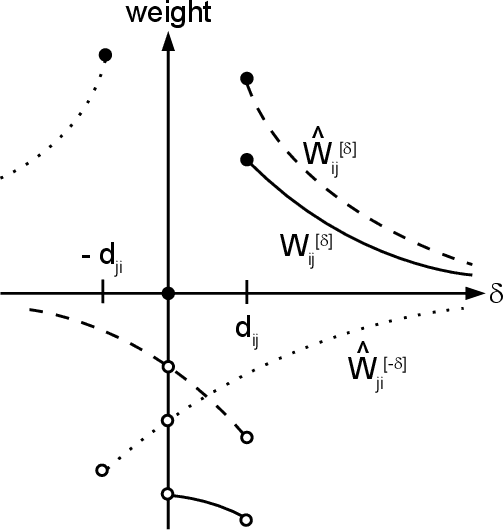
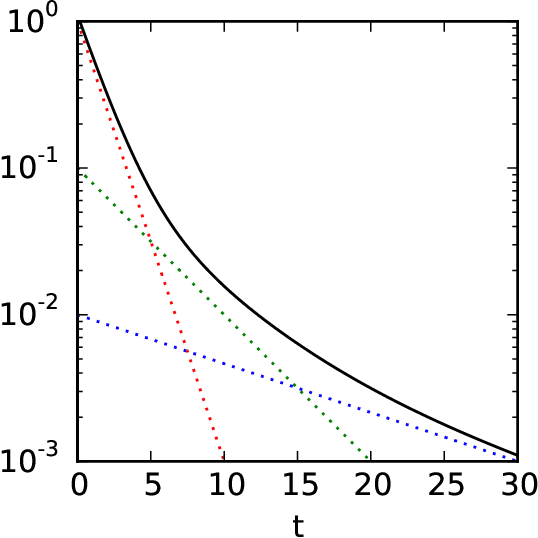
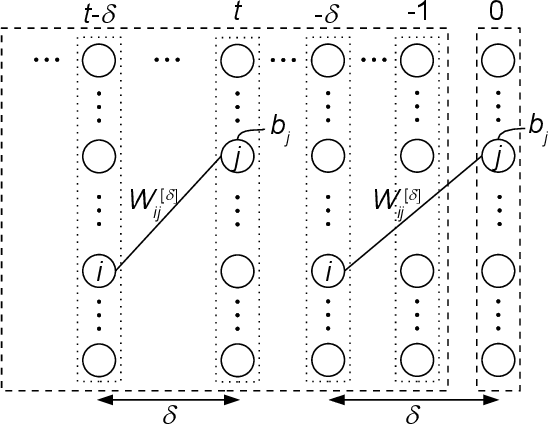
We propose a particularly structured Boltzmann machine, which we refer to as a dynamic Boltzmann machine (DyBM), as a stochastic model of a multi-dimensional time-series. The DyBM can have infinitely many layers of units but allows exact and efficient inference and learning when its parameters have a proposed structure. This proposed structure is motivated by postulates and observations, from biological neural networks, that the synaptic weight is strengthened or weakened, depending on the timing of spikes (i.e., spike-timing dependent plasticity or STDP). We show that the learning rule of updating the parameters of the DyBM in the direction of maximizing the likelihood of given time-series can be interpreted as STDP with long term potentiation and long term depression. The learning rule has a guarantee of convergence and can be performed in a distributed matter (i.e., local in space) with limited memory (i.e., local in time).