Learning dynamic Boltzmann machines with spike-timing dependent plasticity
Paper and Code
Sep 29, 2015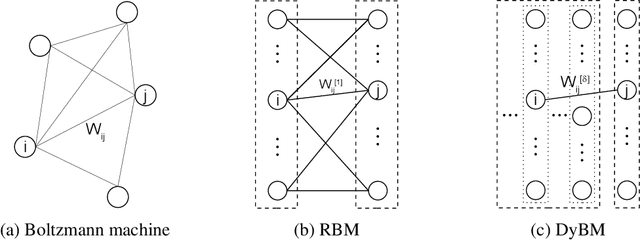
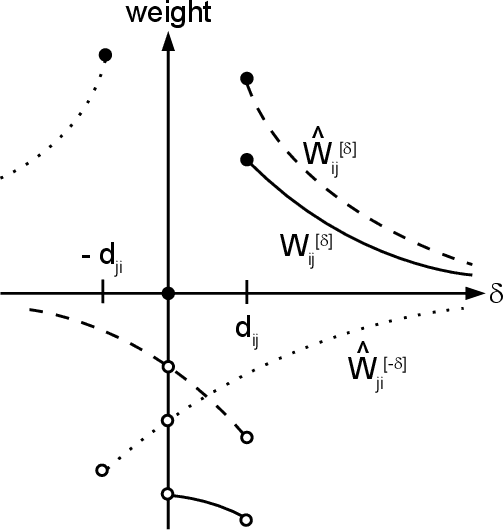
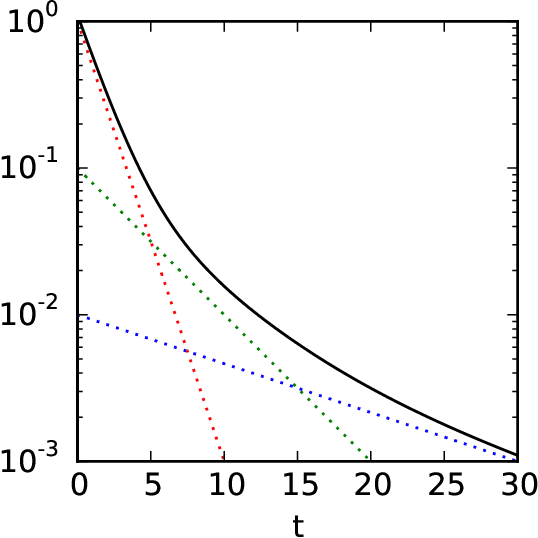
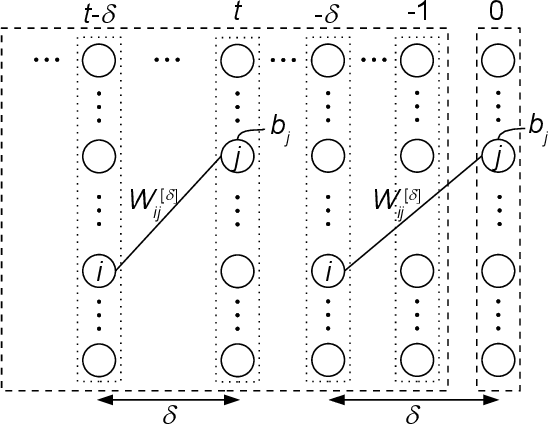
We propose a particularly structured Boltzmann machine, which we refer to as a dynamic Boltzmann machine (DyBM), as a stochastic model of a multi-dimensional time-series. The DyBM can have infinitely many layers of units but allows exact and efficient inference and learning when its parameters have a proposed structure. This proposed structure is motivated by postulates and observations, from biological neural networks, that the synaptic weight is strengthened or weakened, depending on the timing of spikes (i.e., spike-timing dependent plasticity or STDP). We show that the learning rule of updating the parameters of the DyBM in the direction of maximizing the likelihood of given time-series can be interpreted as STDP with long term potentiation and long term depression. The learning rule has a guarantee of convergence and can be performed in a distributed matter (i.e., local in space) with limited memory (i.e., local in time).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge