Mahdi Khodayar
Heterogeneous Multi-Agent Proximal Policy Optimization for Power Distribution System Restoration
Nov 18, 2025Abstract:Restoring power distribution systems (PDS) after large-scale outages requires sequential switching operations that reconfigure feeder topology and coordinate distributed energy resources (DERs) under nonlinear constraints such as power balance, voltage limits, and thermal ratings. These challenges make conventional optimization and value-based RL approaches computationally inefficient and difficult to scale. This paper applies a Heterogeneous-Agent Reinforcement Learning (HARL) framework, instantiated through Heterogeneous-Agent Proximal Policy Optimization (HAPPO), to enable coordinated restoration across interconnected microgrids. Each agent controls a distinct microgrid with different loads, DER capacities, and switch counts, introducing practical structural heterogeneity. Decentralized actor policies are trained with a centralized critic to compute advantage values for stable on-policy updates. A physics-informed OpenDSS environment provides full power flow feedback and enforces operational limits via differentiable penalty signals rather than invalid action masking. The total DER generation is capped at 2400 kW, and each microgrid must satisfy local supply-demand feasibility. Experiments on the IEEE 123-bus and IEEE 8500-node systems show that HAPPO achieves faster convergence, higher restored power, and smoother multi-seed training than DQN, PPO, MAES, MAGDPG, MADQN, Mean-Field RL, and QMIX. Results demonstrate that incorporating microgrid-level heterogeneity within the HARL framework yields a scalable, stable, and constraint-aware solution for complex PDS restoration.
A Deep Generative Model for Graphs: Supervised Subset Selection to Create Diverse Realistic Graphs with Applications to Power Networks Synthesis
Jan 17, 2019

Abstract:Creating and modeling real-world graphs is a crucial problem in various applications of engineering, biology, and social sciences; however, learning the distributions of nodes/edges and sampling from them to generate realistic graphs is still challenging. Moreover, generating a diverse set of synthetic graphs that all imitate a real network is not addressed. In this paper, the novel problem of creating diverse synthetic graphs is solved. First, we devise the deep supervised subset selection (DeepS3) algorithm; Given a ground-truth set of data points, DeepS3 selects a diverse subset of all items (i.e. data points) that best represent the items in the ground-truth set. Furthermore, we propose the deep graph representation recurrent network (GRRN) as a novel generative model that learns a probabilistic representation of a real weighted graph. Training the GRRN, we generate a large set of synthetic graphs that are likely to follow the same features and adjacency patterns as the original one. Incorporating GRRN with DeepS3, we select a diverse subset of generated graphs that best represent the behaviors of the real graph (i.e. our ground-truth). We apply our model to the novel problem of power grid synthesis, where a synthetic power network is created with the same physical/geometric properties as a real power system without revealing the real locations of the substations (nodes) and the lines (edges), since such data is confidential. Experiments on the Synthetic Power Grid Data Set show accurate synthetic networks that follow similar structural and spatial properties as the real power grid.
Convolutional Graph Auto-encoder: A Deep Generative Neural Architecture for Probabilistic Spatio-temporal Solar Irradiance Forecasting
Sep 10, 2018
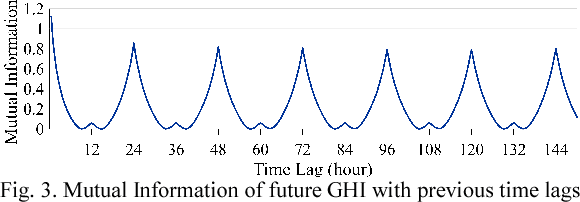


Abstract:Machine Learning on graph-structured data is an important and omnipresent task for a vast variety of applications including anomaly detection and dynamic network analysis. In this paper, a deep generative model is introduced to capture continuous probability densities corresponding to the nodes of an arbitrary graph. In contrast to all learning formulations in the area of discriminative pattern recognition, we propose a scalable generative optimization/algorithm theoretically proved to capture distributions at the nodes of a graph. Our model is able to generate samples from the probability densities learned at each node. This probabilistic data generation model, i.e. convolutional graph auto-encoder (CGAE), is devised based on the localized first-order approximation of spectral graph convolutions, deep learning, and the variational Bayesian inference. We apply our CGAE to a new problem, the spatio-temporal probabilistic solar irradiance prediction. Multiple solar radiation measurement sites in a wide area in northern states of the US are modeled as an undirected graph. Using our proposed model, the distribution of future irradiance given historical radiation observations is estimated for every site/node. Numerical results on the National Solar Radiation Database show state-of-the-art performance for probabilistic radiation prediction on geographically distributed irradiance data in terms of reliability, sharpness, and continuous ranked probability score.
Energy Disaggregation via Deep Temporal Dictionary Learning
Sep 10, 2018



Abstract:This paper addresses the energy disaggregation problem, i.e. decomposing the electricity signal of a whole home to its operating devices. First, we cast the problem as a dictionary learning (DL) problem where the key electricity patterns representing consumption behaviors are extracted for each device and stored in a dictionary matrix. The electricity signal of each device is then modeled by a linear combination of such patterns with sparse coefficients that determine the contribution of each device in the total electricity. Although popular, the classic DL approach is prone to high error in real-world applications including energy disaggregation, as it merely finds linear dictionaries. Moreover, this method lacks a recurrent structure; thus, it is unable to leverage the temporal structure of energy signals. Motivated by such shortcomings, we propose a novel optimization program where the dictionary and its sparse coefficients are optimized simultaneously with a deep neural model extracting powerful nonlinear features from the energy signals. A long short-term memory auto-encoder (LSTM-AE) is proposed with tunable time dependent states to capture the temporal behavior of energy signals for each device. We learn the dictionary in the space of temporal features captured by the LSTM-AE rather than the original space of the energy signals; hence, in contrast to the traditional DL, here, a nonlinear dictionary is learned using powerful temporal features extracted from our deep model. Real experiments on the publicly available Reference Energy Disaggregation Dataset (REDD) show significant improvement compared to the state-of-the-art methodologies in terms of the disaggregation accuracy and F-score metrics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge