Extended target tracking utilizing machine-learning software -- with applications to animal classification

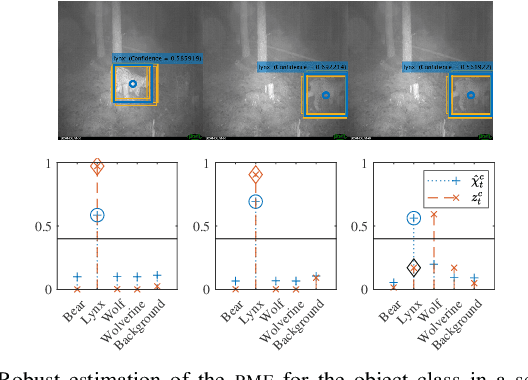
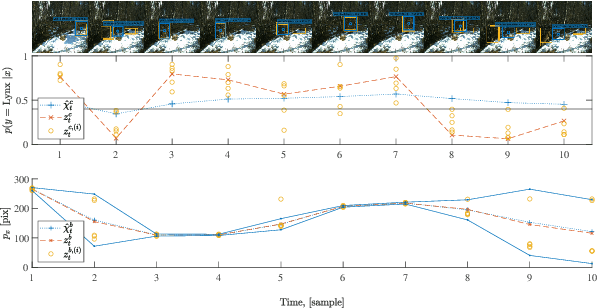
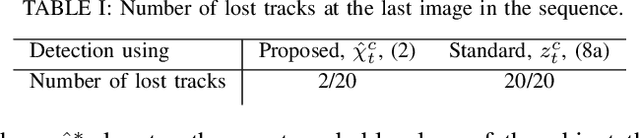
This paper considers the problem of detecting and tracking objects in a sequence of images. The problem is formulated in a filtering framework, using the output of object-detection algorithms as measurements. An extension to the filtering formulation is proposed that incorporates class information from the previous frame to robustify the classification, even if the object-detection algorithm outputs an incorrect prediction. Further, the properties of the object-detection algorithm are exploited to quantify the uncertainty of the bounding box detection in each frame. The complete filtering method is evaluated on camera trap images of the four large Swedish carnivores, bear, lynx, wolf, and wolverine. The experiments show that the class tracking formulation leads to a more robust classification.

Fusion framework and multimodality for the Laplacian approximation of Bayesian neural networks

This paper considers the problem of sequential fusion of predictions from neural networks (NN) and fusion of predictions from multiple NN. This fusion strategy increases the robustness, i.e., reduces the impact of one incorrect classification and detection of outliers the \nn has not seen during training. This paper uses Laplacian approximation of Bayesian NNs (BNNs) to quantify the uncertainty necessary for fusion. Here, an extension is proposed such that the prediction of the NN can be represented by multimodal distributions. Regarding calibration of the estimated uncertainty in the prediction, the performance is significantly improved by having the flexibility to represent a multimodal distribution. Two class classical image classification tasks, i.e., MNIST and CFAR10, and image sequences from camera traps of carnivores in Swedish forests have been used to demonstrate the fusion strategies and proposed extension to the Laplacian approximation.

Uncertainty quantification in neural network classifiers -- a local linear approach

Classifiers based on neural networks (NN) often lack a measure of uncertainty in the predicted class. We propose a method to estimate the probability mass function (PMF) of the different classes, as well as the covariance of the estimated PMF. First, a local linear approach is used during the training phase to recursively compute the covariance of the parameters in the NN. Secondly, in the classification phase another local linear approach is used to propagate the covariance of the learned NN parameters to the uncertainty in the output of the last layer of the NN. This allows for an efficient Monte Carlo (MC) approach for: (i) estimating the PMF; (ii) calculating the covariance of the estimated PMF; and (iii) proper risk assessment and fusion of multiple classifiers. Two classical image classification tasks, i.e., MNIST, and CFAR10, are used to demonstrate the efficiency the proposed method.