Noise-Aware Optimization in Nominally Identical Manufacturing and Measuring Systems for High-Throughput Parallel Workflows

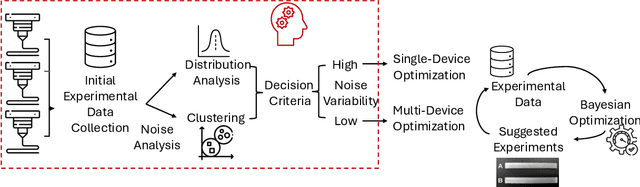
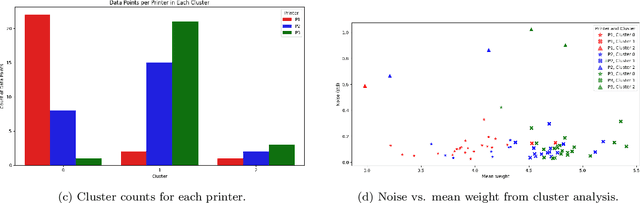
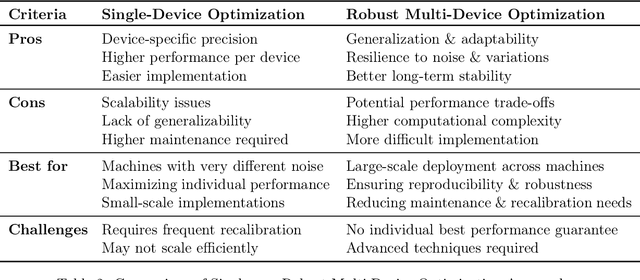
Device-to-device variability in experimental noise critically impacts reproducibility, especially in automated, high-throughput systems like additive manufacturing farms. While manageable in small labs, such variability can escalate into serious risks at larger scales, such as architectural 3D printing, where noise may cause structural or economic failures. This contribution presents a noise-aware decision-making algorithm that quantifies and models device-specific noise profiles to manage variability adaptively. It uses distributional analysis and pairwise divergence metrics with clustering to choose between single-device and robust multi-device Bayesian optimization strategies. Unlike conventional methods that assume homogeneous devices or generic robustness, this framework explicitly leverages inter-device differences to enhance performance, reproducibility, and efficiency. An experimental case study involving three nominally identical 3D printers (same brand, model, and close serial numbers) demonstrates reduced redundancy, lower resource usage, and improved reliability. Overall, this framework establishes a paradigm for precision- and resource-aware optimization in scalable, automated experimental platforms.

Model-Based Reinforcement Learning Control of Reaction-Diffusion Problems

Mathematical and computational tools have proven to be reliable in decision-making processes. In recent times, in particular, machine learning-based methods are becoming increasingly popular as advanced support tools. When dealing with control problems, reinforcement learning has been applied to decision-making in several applications, most notably in games. The success of these methods in finding solutions to complex problems motivates the exploration of new areas where they can be employed to overcome current difficulties. In this paper, we explore the use of automatic control strategies to initial boundary value problems in thermal and disease transport. Specifically, in this work, we adapt an existing reinforcement learning algorithm using a stochastic policy gradient method and we introduce two novel reward functions to drive the flow of the transported field. The new model-based framework exploits the interactions between a reaction-diffusion model and the modified agent. The results show that certain controls can be implemented successfully in these applications, although model simplifications had to be assumed.

Topological Descriptors Help Predict Guest Adsorption in Nanoporous Materials

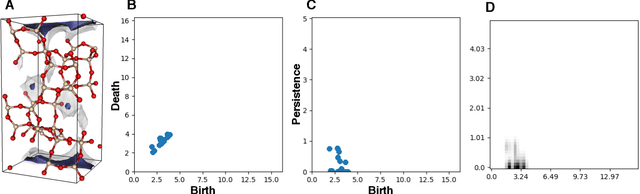
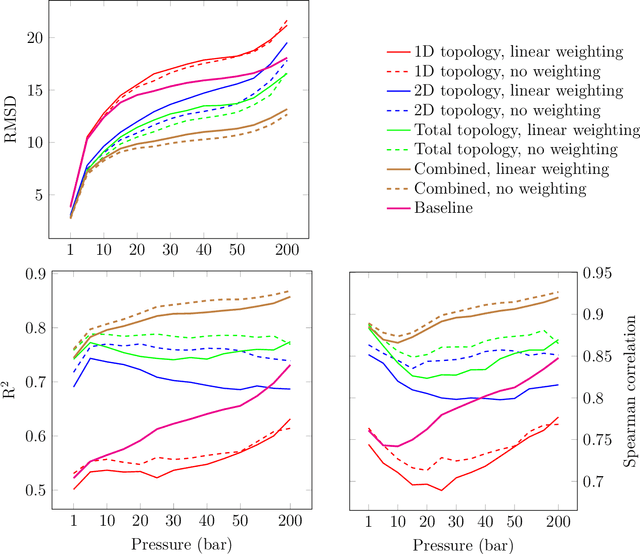
Machine learning has emerged as an attractive alternative to experiments and simulations for predicting material properties. Usually, such an approach relies on specific domain knowledge for feature design: each learning target requires careful selection of features that an expert recognizes as important for the specific task. The major drawback of this approach is that computation of only a few structural features has been implemented so far, and it is difficult to tell a priori which features are important for a particular application. The latter problem has been empirically observed for predictors of guest uptake in nanoporous materials: local and global porosity features become dominant descriptors at low and high pressures, respectively. We investigate a feature representation of materials using tools from topological data analysis. Specifically, we use persistent homology to describe the geometry of nanoporous materials at various scales. We combine our topological descriptor with traditional structural features and investigate the relative importance of each to the prediction tasks. We demonstrate an application of this feature representation by predicting methane adsorption in zeolites, for pressures in the range of 1-200 bar. Our results not only show a considerable improvement compared to the baseline, but they also highlight that topological features capture information complementary to the structural features, which is especially important for the adsorption at low pressure, a task particularly difficult for the traditional features.