Learn on Source, Refine on Target:A Model Transfer Learning Framework with Random Forests

We propose novel model transfer-learning methods that refine a decision forest model M learned within a "source" domain using a training set sampled from a "target" domain, assumed to be a variation of the source. We present two random forest transfer algorithms. The first algorithm searches greedily for locally optimal modifications of each tree structure by trying to locally expand or reduce the tree around individual nodes. The second algorithm does not modify structure, but only the parameter (thresholds) associated with decision nodes. We also propose to combine both methods by considering an ensemble that contains the union of the two forests. The proposed methods exhibit impressive experimental results over a range of problems.

The Perturbed Variation

We introduce a new discrepancy score between two distributions that gives an indication on their similarity. While much research has been done to determine if two samples come from exactly the same distribution, much less research considered the problem of determining if two finite samples come from similar distributions. The new score gives an intuitive interpretation of similarity; it optimally perturbs the distributions so that they best fit each other. The score is defined between distributions, and can be efficiently estimated from samples. We provide convergence bounds of the estimated score, and develop hypothesis testing procedures that test if two data sets come from similar distributions. The statistical power of this procedures is presented in simulations. We also compare the score's capacity to detect similarity with that of other known measures on real data.

Learning from Multiple Outlooks

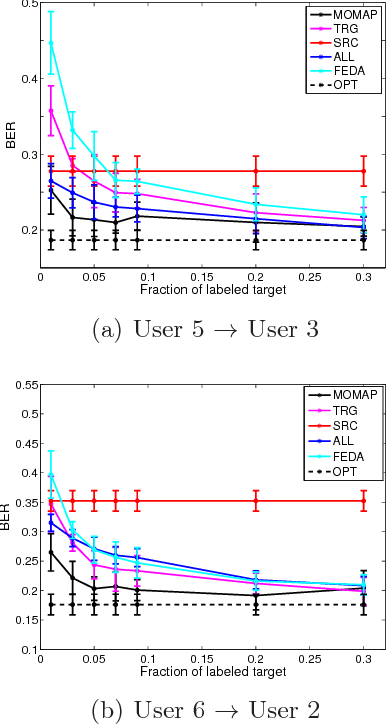
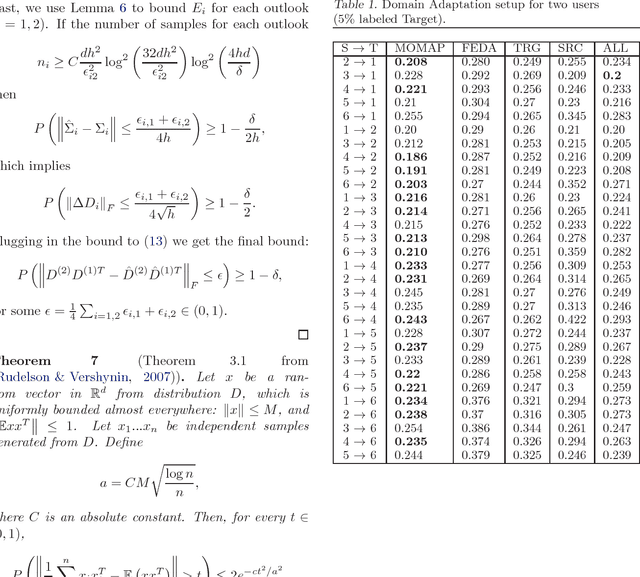
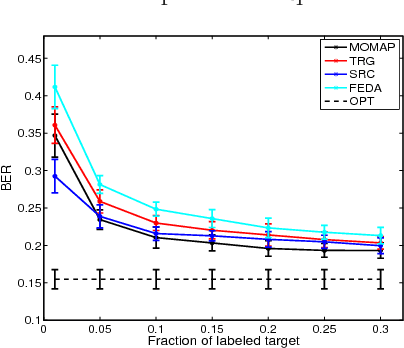
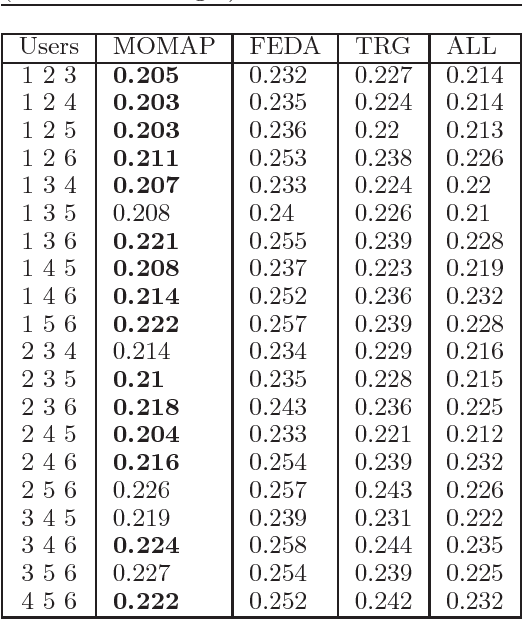
We propose a novel problem formulation of learning a single task when the data are provided in different feature spaces. Each such space is called an outlook, and is assumed to contain both labeled and unlabeled data. The objective is to take advantage of the data from all the outlooks to better classify each of the outlooks. We devise an algorithm that computes optimal affine mappings from different outlooks to a target outlook by matching moments of the empirical distributions. We further derive a probabilistic interpretation of the resulting algorithm and a sample complexity bound indicating how many samples are needed to adequately find the mapping. We report the results of extensive experiments on activity recognition tasks that show the value of the proposed approach in boosting performance.