Learning from Multiple Outlooks
Paper and Code
Jun 14, 2011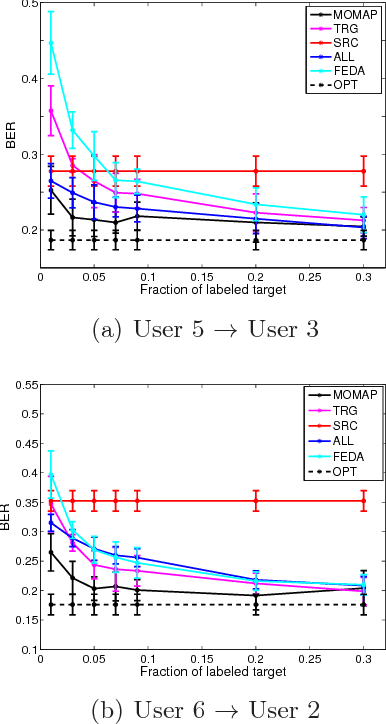
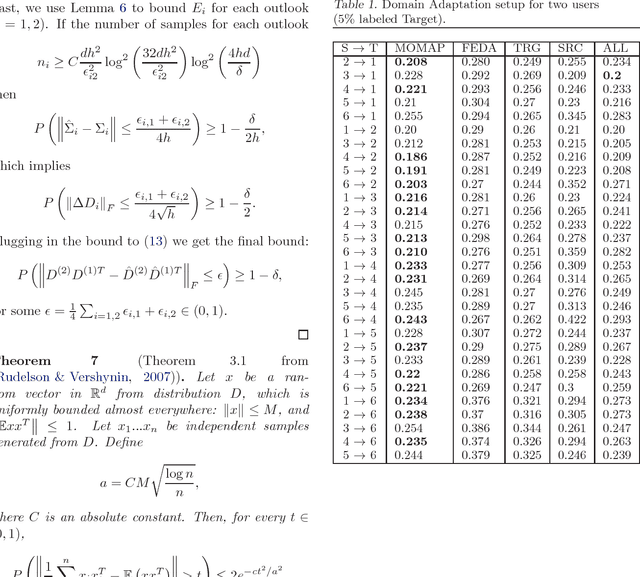
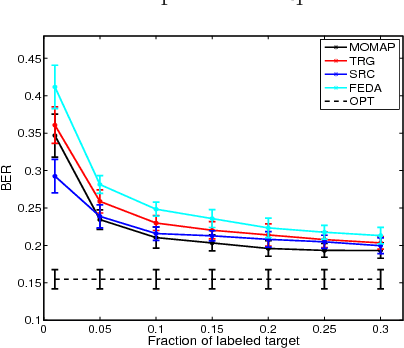
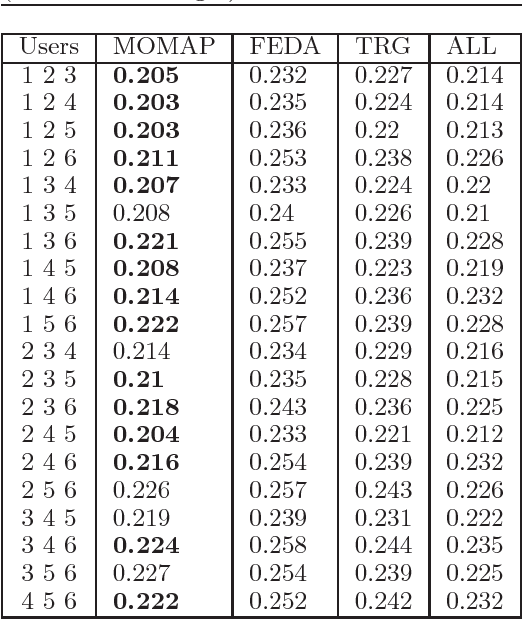
We propose a novel problem formulation of learning a single task when the data are provided in different feature spaces. Each such space is called an outlook, and is assumed to contain both labeled and unlabeled data. The objective is to take advantage of the data from all the outlooks to better classify each of the outlooks. We devise an algorithm that computes optimal affine mappings from different outlooks to a target outlook by matching moments of the empirical distributions. We further derive a probabilistic interpretation of the resulting algorithm and a sample complexity bound indicating how many samples are needed to adequately find the mapping. We report the results of extensive experiments on activity recognition tasks that show the value of the proposed approach in boosting performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge