Min-similarity association rules for identifying past comorbidities of recurrent ED and inpatient patients

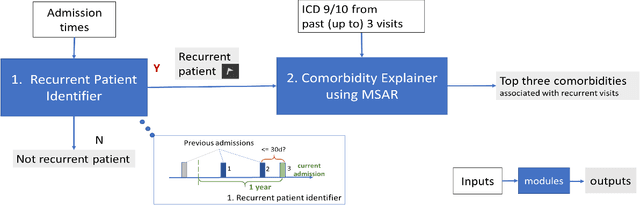
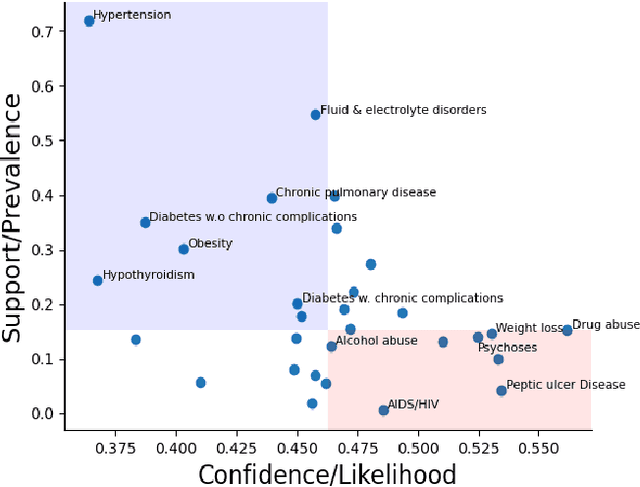
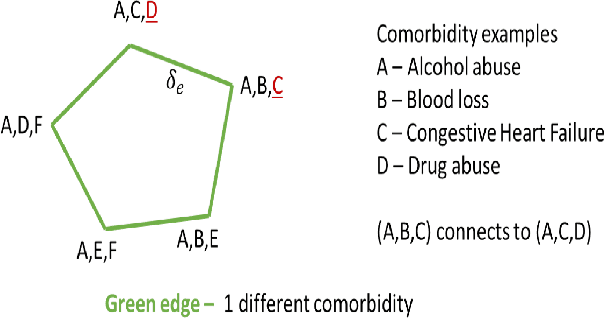
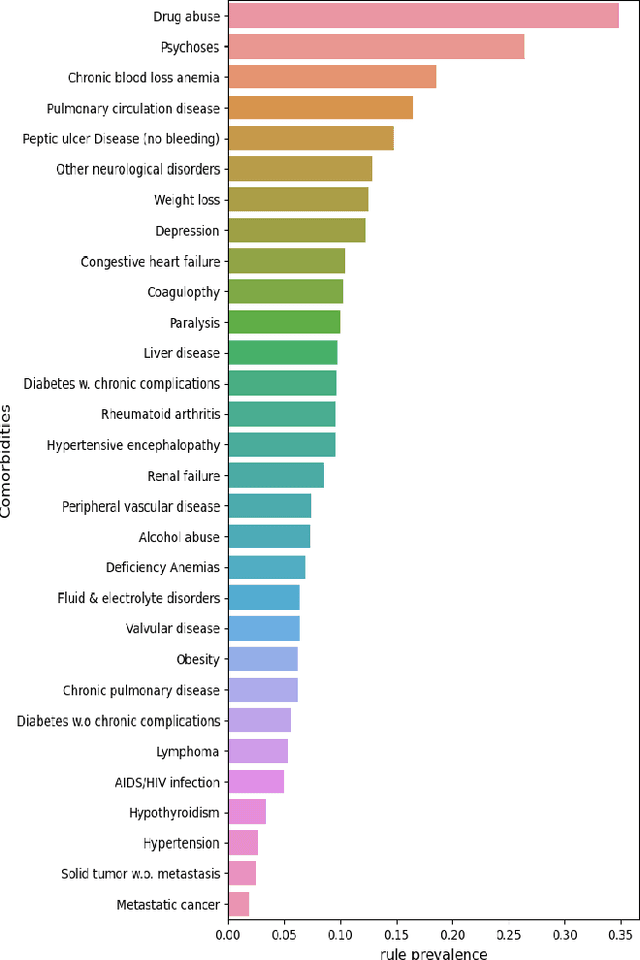
In the hospital setting, a small percentage of recurrent frequent patients contribute to a disproportional amount of healthcare resource usage. Moreover, in many of these cases, patient outcomes can be greatly improved by reducing reoccurring visits, especially when they are associated with substance abuse, mental health, and medical factors that could be improved by social-behavioral interventions, outpatient or preventative care. To address this, we developed a computationally efficient and interpretable framework that both identifies recurrent patients with high utilization and determines which comorbidities contribute most to their recurrent visits. Specifically, we present a novel algorithm, called the minimum similarity association rules (MSAR), balancing confidence-support trade-off, to determine the conditions most associated with reoccurring Emergency department (ED) and inpatient visits. We validate MSAR on a large Electric Health Record (EHR) dataset. Part of the solution is deployed in Philips product Patient Flow Capacity Suite (PFCS).

Reducing Sampling Ratios and Increasing Number of Estimates Improve Bagging in Sparse Regression

Bagging, a powerful ensemble method from machine learning, improves the performance of unstable predictors. Although the power of Bagging has been shown mostly in classification problems, we demonstrate the success of employing Bagging in sparse regression over the baseline method (L1 minimization). The framework employs the generalized version of the original Bagging with various bootstrap ratios. The performance limits associated with different choices of bootstrap sampling ratio L/m and number of estimates K is analyzed theoretically. Simulation shows that the proposed method yields state-of-the-art recovery performance, outperforming L1 minimization and Bolasso in the challenging case of low levels of measurements. A lower L/m ratio (60% - 90%) leads to better performance, especially with a small number of measurements. With the reduced sampling rate, SNR improves over the original Bagging by up to 24%. With a properly chosen sampling ratio, a reasonably small number of estimates K = 30 gives satisfying result, even though increasing K is discovered to always improve or at least maintain the performance.

JOBS: Joint-Sparse Optimization from Bootstrap Samples

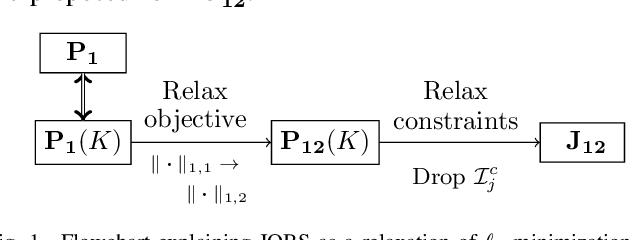
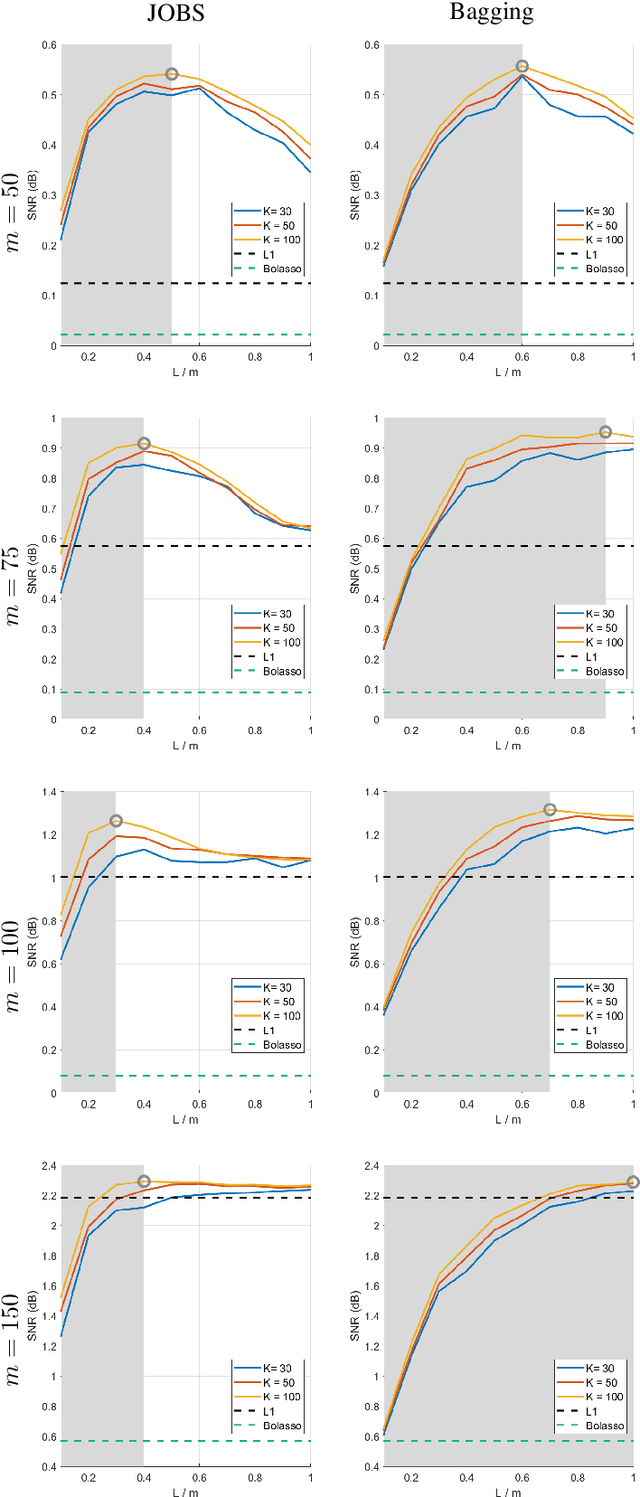
Classical signal recovery based on $\ell_1$ minimization solves the least squares problem with all available measurements via sparsity-promoting regularization. In practice, it is often the case that not all measurements are available or required for recovery. Measurements might be corrupted/missing or they arrive sequentially in streaming fashion. In this paper, we propose a global sparse recovery strategy based on subsets of measurements, named JOBS, in which multiple measurements vectors are generated from the original pool of measurements via bootstrapping, and then a joint-sparse constraint is enforced to ensure support consistency among multiple predictors. The final estimate is obtained by averaging over the $K$ predictors. The performance limits associated with different choices of number of bootstrap samples $L$ and number of estimates $K$ is analyzed theoretically. Simulation results validate some of the theoretical analysis, and show that the proposed method yields state-of-the-art recovery performance, outperforming $\ell_1$ minimization and a few other existing bootstrap-based techniques in the challenging case of low levels of measurements and is preferable over other bagging-based methods in the streaming setting since it performs better with small $K$ and $L$ for data-sets with large sizes.