Thermal-LiDAR Fusion for Robust Tunnel Localization in GNSS-Denied and Low-Visibility Conditions

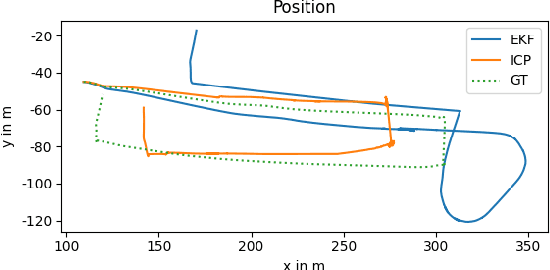
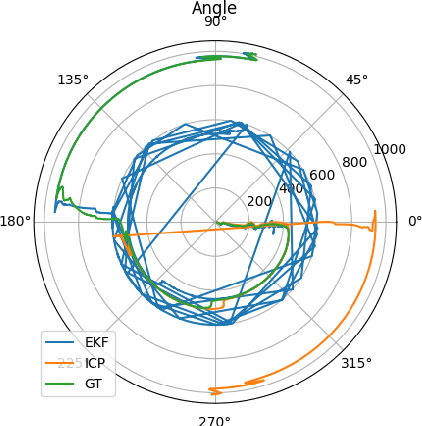
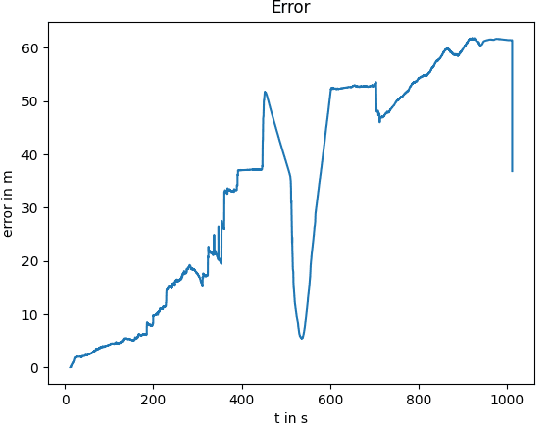
Despite significant progress in autonomous navigation, a critical gap remains in ensuring reliable localization in hazardous environments such as tunnels, urban disaster zones, and underground structures. Tunnels present a uniquely difficult scenario: they are not only prone to GNSS signal loss, but also provide little features for visual localization due to their repetitive walls and poor lighting. These conditions degrade conventional vision-based and LiDAR-based systems, which rely on distinguishable environmental features. To address this, we propose a novel sensor fusion framework that integrates a thermal camera with a LiDAR to enable robust localization in tunnels and other perceptually degraded environments. The thermal camera provides resilience in low-light or smoke conditions, while the LiDAR delivers precise depth perception and structural awareness. By combining these sensors, our framework ensures continuous and accurate localization across diverse and dynamic environments. We use an Extended Kalman Filter (EKF) to fuse multi-sensor inputs, and leverages visual odometry and SLAM (Simultaneous Localization and Mapping) techniques to process the sensor data, enabling robust motion estimation and mapping even in GNSS-denied environments. This fusion of sensor modalities not only enhances system resilience but also provides a scalable solution for cyber-physical systems in connected and autonomous vehicles (CAVs). To validate the framework, we conduct tests in a tunnel environment, simulating sensor degradation and visibility challenges. The results demonstrate that our method sustains accurate localization where standard approaches deteriorate due to the tunnels featureless geometry. The frameworks versatility makes it a promising solution for autonomous vehicles, inspection robots, and other cyber-physical systems operating in constrained, perceptually poor environments.

A Cost-Effective Approach to Smooth A* Path Planning for Autonomous Vehicles

Path planning for wheeled mobile robots is a critical component in the field of automation and intelligent transportation systems. Car-like vehicles, which have non-holonomic constraints on their movement capability impose additional requirements on the planned paths. Traditional path planning algorithms, such as A* , are widely used due to their simplicity and effectiveness in finding optimal paths in complex environments. However, these algorithms often do not consider vehicle dynamics, resulting in paths that are infeasible or impractical for actual driving. Specifically, a path that minimizes the number of grid cells may still be too curvy or sharp for a car-like vehicle to navigate smoothly. This paper addresses the need for a path planning solution that not only finds a feasible path but also ensures that the path is smooth and drivable. By adapting the A* algorithm for a curvature constraint and incorporating a cost function that considers the smoothness of possible paths, we aim to bridge the gap between grid based path planning and smooth paths that are drivable by car-like vehicles. The proposed method leverages motion primitives, pre-computed using a ribbon based path planner that produces smooth paths of minimum curvature. The motion primitives guide the A* algorithm in finding paths of minimal length and curvature. With the proposed modification on the A* algorithm, the planned paths can be constraint to have a minimum turning radius much larger than the grid size. We demonstrate the effectiveness of the proposed algorithm in different unstructured environments. In a two-stage planning approach, first the modified A* algorithm finds a grid-based path and the ribbon based path planner creates a smooth path within the area of grid cells. The resulting paths are smooth with small curvatures independent of the orientation of the grid axes and even in presence of sharp obstacles.