Collaborative Learning From Distributed Data With Differentially Private Synthetic Twin Data

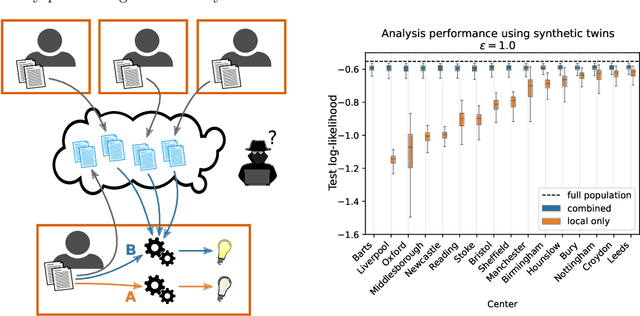
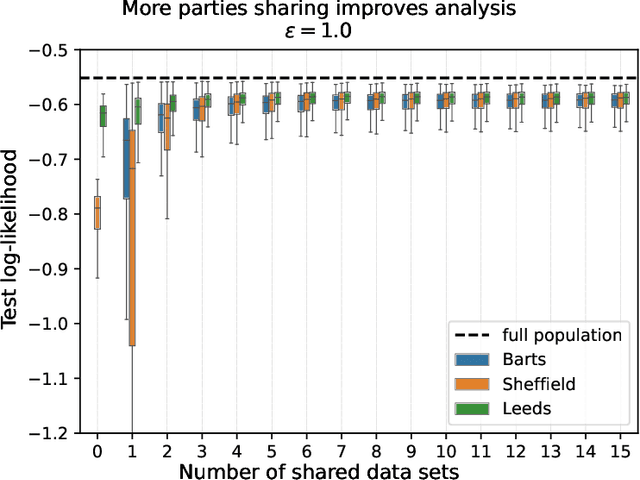
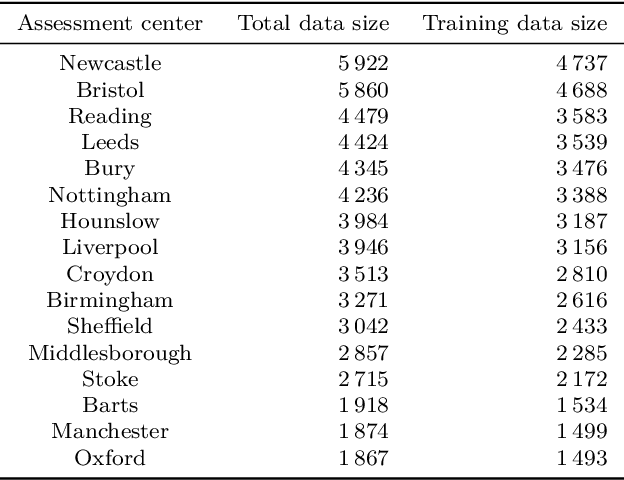
Consider a setting where multiple parties holding sensitive data aim to collaboratively learn population level statistics, but pooling the sensitive data sets is not possible. We propose a framework in which each party shares a differentially private synthetic twin of their data. We study the feasibility of combining such synthetic twin data sets for collaborative learning on real-world health data from the UK Biobank. We discover that parties engaging in the collaborative learning via shared synthetic data obtain more accurate estimates of target statistics compared to using only their local data. This finding extends to the difficult case of small heterogeneous data sets. Furthermore, the more parties participate, the larger and more consistent the improvements become. Finally, we find that data sharing can especially help parties whose data contain underrepresented groups to perform better-adjusted analysis for said groups. Based on our results we conclude that sharing of synthetic twins is a viable method for enabling learning from sensitive data without violating privacy constraints even if individual data sets are small or do not represent the overall population well. The setting of distributed sensitive data is often a bottleneck in biomedical research, which our study shows can be alleviated with privacy-preserving collaborative learning methods.

DPVIm: Differentially Private Variational Inference Improved

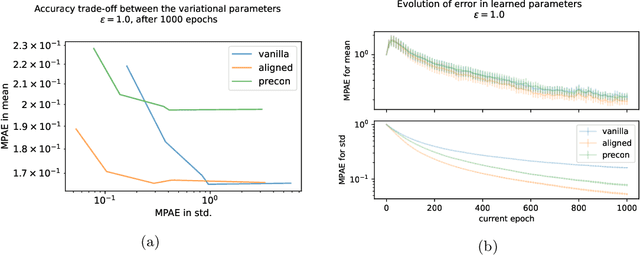
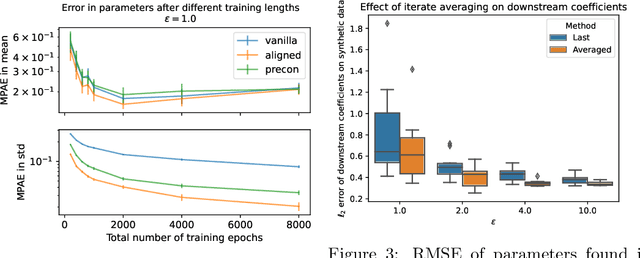
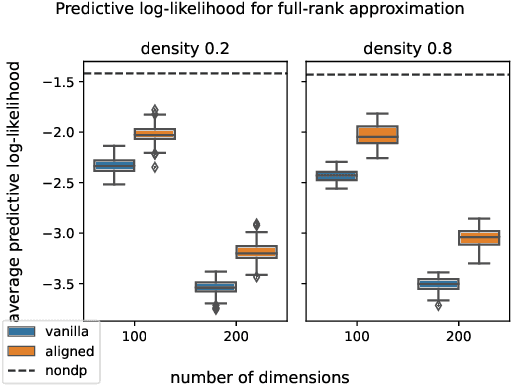
Differentially private (DP) release of multidimensional statistics typically considers an aggregate sensitivity, e.g. the vector norm of a high-dimensional vector. However, different dimensions of that vector might have widely different magnitudes and therefore DP perturbation disproportionately affects the signal across dimensions. We observe this problem in the gradient release of the DP-SGD algorithm when using it for variational inference (VI), where it manifests in poor convergence as well as high variance in outputs for certain variational parameters, and make the following contributions: (i) We mathematically isolate the cause for the difference in magnitudes between gradient parts corresponding to different variational parameters. Using this as prior knowledge we establish a link between the gradients of the variational parameters, and propose an efficient while simple fix for the problem to obtain a less noisy gradient estimator, which we call $\textit{aligned}$ gradients. This approach allows us to obtain the updates for the covariance parameter of a Gaussian posterior approximation without a privacy cost. We compare this to alternative approaches for scaling the gradients using analytically derived preconditioning, e.g. natural gradients. (ii) We suggest using iterate averaging over the DP parameter traces recovered during the training, to reduce the DP-induced noise in parameter estimates at no additional cost in privacy. Finally, (iii) to accurately capture the additional uncertainty DP introduces to the model parameters, we infer the DP-induced noise from the parameter traces and include that in the learned posteriors to make them $\textit{noise aware}$. We demonstrate the efficacy of our proposed improvements through various experiments on real data.

d3p -- A Python Package for Differentially-Private Probabilistic Programming

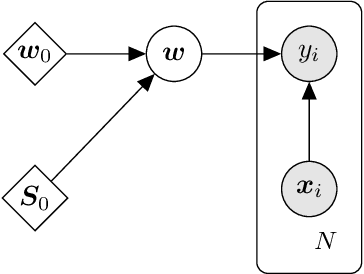
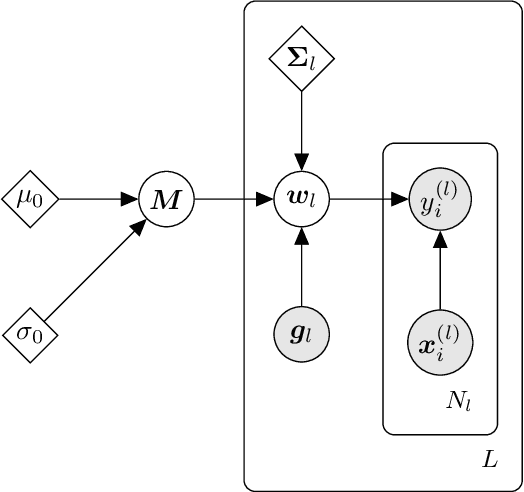
We present d3p, a software package designed to help fielding runtime efficient widely-applicable Bayesian inference under differential privacy guarantees. d3p achieves general applicability to a wide range of probabilistic modelling problems by implementing the differentially private variational inference algorithm, allowing users to fit any parametric probabilistic model with a differentiable density function. d3p adopts the probabilistic programming paradigm as a powerful way for the user to flexibly define such models. We demonstrate the use of our software on a hierarchical logistic regression example, showing the expressiveness of the modelling approach as well as the ease of running the parameter inference. We also perform an empirical evaluation of the runtime of the private inference on a complex model and find an $\sim$10 fold speed-up compared to an implementation using TensorFlow Privacy.

Tight Approximate Differential Privacy for Discrete-Valued Mechanisms Using FFT

We propose a numerical accountant for evaluating the tight $(\varepsilon,\delta)$-privacy loss for algorithms with discrete one-dimensional output. The method is based on the privacy loss distribution formalism and it is able to exploit the recently introduced Fast Fourier Transform based accounting technique. We carry out a complete error analysis of the method in terms of the moment bounds for the numerical estimate of the privacy loss distribution. We demonstrate the performance on the binomial mechanism and show that our approach allows decreasing noise variance up to an order of magnitude at equal privacy compared to existing bounds in the literature. We also give a novel approach for evaluating $(\varepsilon,\delta)$-upper bound for the subsampled Gaussian mechanism. This completes the previously proposed analysis by giving a strict upper bound for $(\varepsilon,\delta)$. We also illustrate how to compute tight bounds for the exponential mechanism applied to counting queries.