Calibration and Uncertainty Quantification of Bayesian Convolutional Neural Networks for Geophysical Applications

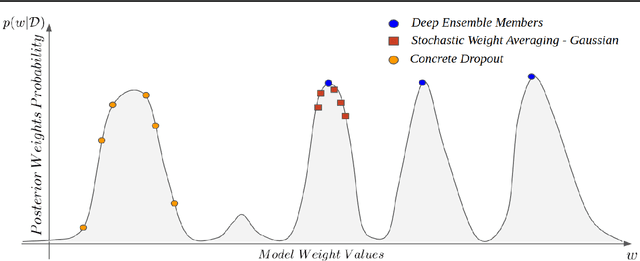
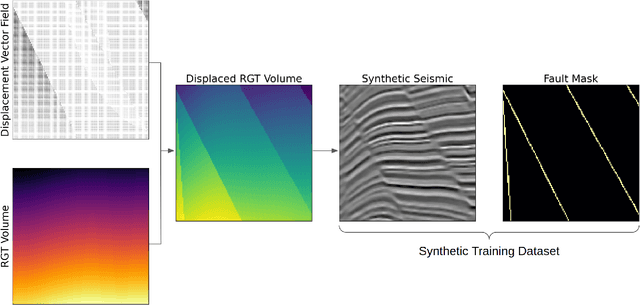
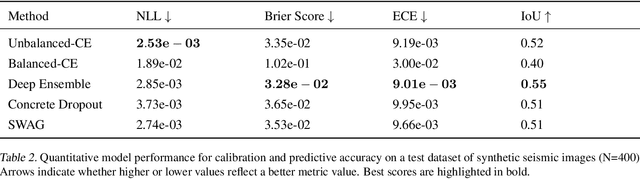
Deep neural networks offer numerous potential applications across geoscience, for example, one could argue that they are the state-of-the-art method for predicting faults in seismic datasets. In quantitative reservoir characterization workflows, it is common to incorporate the uncertainty of predictions thus such subsurface models should provide calibrated probabilities and the associated uncertainties in their predictions. It has been shown that popular Deep Learning-based models are often miscalibrated, and due to their deterministic nature, provide no means to interpret the uncertainty of their predictions. We compare three different approaches to obtaining probabilistic models based on convolutional neural networks in a Bayesian formalism, namely Deep Ensembles, Concrete Dropout, and Stochastic Weight Averaging-Gaussian (SWAG). These methods are consistently applied to fault detection case studies where Deep Ensembles use independently trained models to provide fault probabilities, Concrete Dropout represents an extension to the popular Dropout technique to approximate Bayesian neural networks, and finally, we apply SWAG, a recent method that is based on the Bayesian inference equivalence of mini-batch Stochastic Gradient Descent. We provide quantitative results in terms of model calibration and uncertainty representation, as well as qualitative results on synthetic and real seismic datasets. Our results show that the approximate Bayesian methods, Concrete Dropout and SWAG, both provide well-calibrated predictions and uncertainty attributes at a lower computational cost when compared to the baseline Deep Ensemble approach. The resulting uncertainties also offer a possibility to further improve the model performance as well as enhancing the interpretability of the models.

Stochastic reconstruction of periodic, three-dimensional multi-phase electrode microstructures using generative adversarial networks

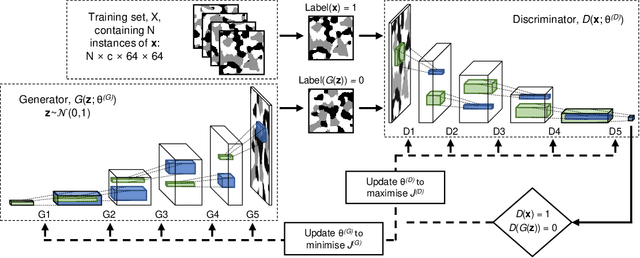
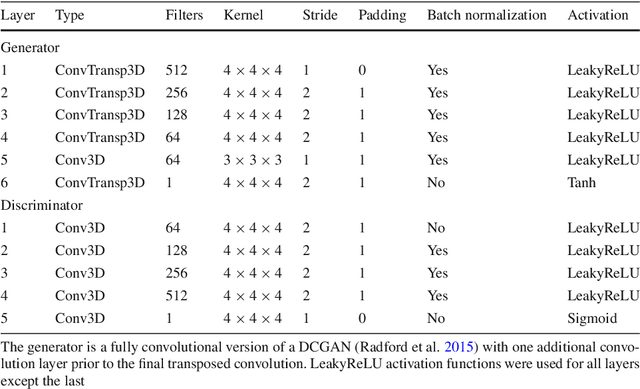
The generation of multiphase porous electrode microstructures is a critical step in the optimisation of electrochemical energy storage devices. This work implements a deep convolutional generative adversarial network (DC-GAN) for generating realistic n-phase microstructural data. The same network architecture is successfully applied to two very different three-phase microstructures: A lithium-ion battery cathode and a solid oxide fuel cell anode. A comparison between the real and synthetic data is performed in terms of the morphological properties (volume fraction, specific surface area, triple-phase boundary) and transport properties (relative diffusivity), as well as the two-point correlation function. The results show excellent agreement between for datasets and they are also visually indistinguishable. By modifying the input to the generator, we show that it is possible to generate microstructure with periodic boundaries in all three directions. This has the potential to significantly reduce the simulated volume required to be considered representative and therefore massively reduce the computational cost of the electrochemical simulations necessary to predict the performance of a particular microstructure during optimisation.

DeepFlow: History Matching in the Space of Deep Generative Models

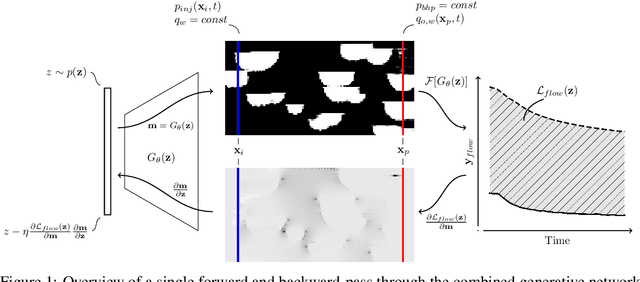
The calibration of a reservoir model with observed transient data of fluid pressures and rates is a key task in obtaining a predictive model of the flow and transport behaviour of the earth's subsurface. The model calibration task, commonly referred to as "history matching", can be formalised as an ill-posed inverse problem where we aim to find the underlying spatial distribution of petrophysical properties that explain the observed dynamic data. We use a generative adversarial network pretrained on geostatistical object-based models to represent the distribution of rock properties for a synthetic model of a hydrocarbon reservoir. The dynamic behaviour of the reservoir fluids is modelled using a transient two-phase incompressible Darcy formulation. We invert for the underlying reservoir properties by first modeling property distributions using the pre-trained generative model then using the adjoint equations of the forward problem to perform gradient descent on the latent variables that control the output of the generative model. In addition to the dynamic observation data, we include well rock-type constraints by introducing an additional objective function. Our contribution shows that for a synthetic test case, we are able to obtain solutions to the inverse problem by optimising in the latent variable space of a deep generative model, given a set of transient observations of a non-linear forward problem.

Stochastic seismic waveform inversion using generative adversarial networks as a geological prior

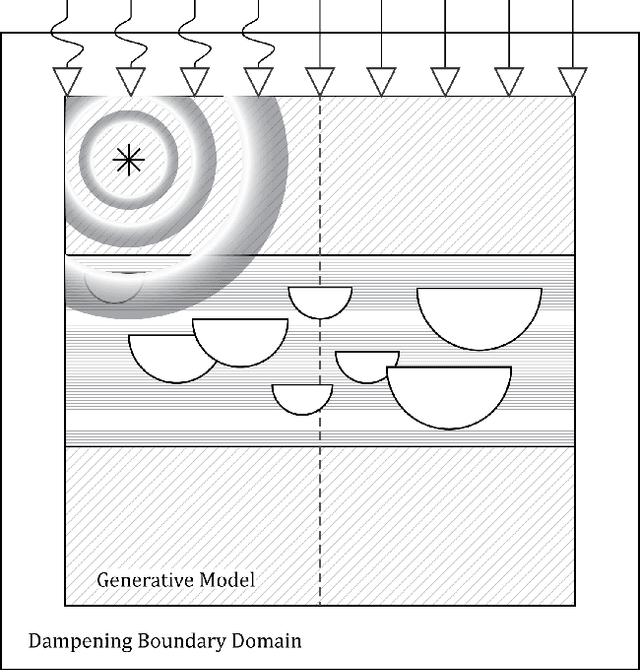
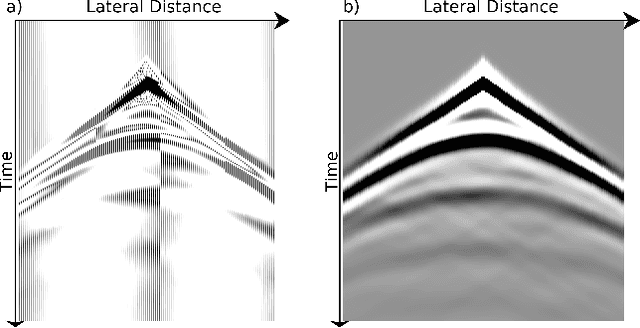
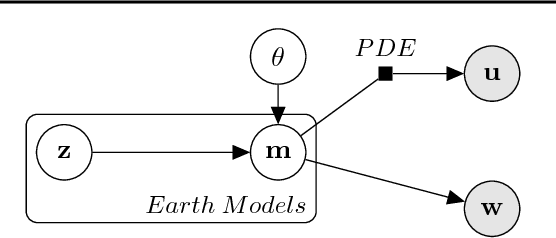
We present an application of deep generative models in the context of partial-differential equation (PDE) constrained inverse problems. We combine a generative adversarial network (GAN) representing an a priori model that creates subsurface geological structures and their petrophysical properties, with the numerical solution of the PDE governing the propagation of acoustic waves within the earth's interior. We perform Bayesian inversion using an approximate Metropolis-adjusted Langevin algorithm (MALA) to sample from the posterior given seismic observations. Gradients with respect to the model parameters governing the forward problem are obtained by solving the adjoint of the acoustic wave equation. Gradients of the mismatch with respect to the latent variables are obtained by leveraging the differentiable nature of the deep neural network used to represent the generative model. We show that approximate MALA sampling allows efficient Bayesian inversion of model parameters obtained from a prior represented by a deep generative model, obtaining a diverse set of realizations that reflect the observed seismic response.

Rapid seismic domain transfer: Seismic velocity inversion and modeling using deep generative neural networks

Traditional physics-based approaches to infer sub-surface properties such as full-waveform inversion or reflectivity inversion are time-consuming and computationally expensive. We present a deep-learning technique that eliminates the need for these computationally complex methods by posing the problem as one of domain transfer. Our solution is based on a deep convolutional generative adversarial network and dramatically reduces computation time. Training based on two different types of synthetic data produced a neural network that generates realistic velocity models when applied to a real dataset. The system's ability to generalize means it is robust against the inherent occurrence of velocity errors and artifacts in both training and test datasets.

Conditioning of three-dimensional generative adversarial networks for pore and reservoir-scale models

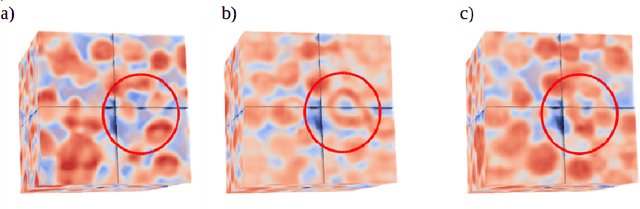
Geostatistical modeling of petrophysical properties is a key step in modern integrated oil and gas reservoir studies. Recently, generative adversarial networks (GAN) have been shown to be a successful method for generating unconditional simulations of pore- and reservoir-scale models. This contribution leverages the differentiable nature of neural networks to extend GANs to the conditional simulation of three-dimensional pore- and reservoir-scale models. Based on the previous work of Yeh et al. (2016), we use a content loss to constrain to the conditioning data and a perceptual loss obtained from the evaluation of the GAN discriminator network. The technique is tested on the generation of three-dimensional micro-CT images of a Ketton limestone constrained by two-dimensional cross-sections, and on the simulation of the Maules Creek alluvial aquifer constrained by one-dimensional sections. Our results show that GANs represent a powerful method for sampling conditioned pore and reservoir samples for stochastic reservoir evaluation workflows.

Stochastic reconstruction of an oolitic limestone by generative adversarial networks

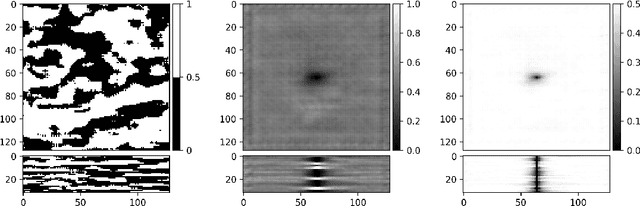
Stochastic image reconstruction is a key part of modern digital rock physics and materials analysis that aims to create numerous representative samples of material micro-structures for upscaling, numerical computation of effective properties and uncertainty quantification. We present a method of three-dimensional stochastic image reconstruction based on generative adversarial neural networks (GANs). GANs represent a framework of unsupervised learning methods that require no a priori inference of the probability distribution associated with the training data. Using a fully convolutional neural network allows fast sampling of large volumetric images.We apply a GAN based workflow of network training and image generation to an oolitic Ketton limestone micro-CT dataset. Minkowski functionals, effective permeability as well as velocity distributions of simulated flow within the acquired images are compared with the synthetic reconstructions generated by the deep neural network. While our results show that GANs allow a fast and accurate reconstruction of the evaluated image dataset, we address a number of open questions and challenges involved in the evaluation of generative network-based methods.

Reconstruction of three-dimensional porous media using generative adversarial neural networks

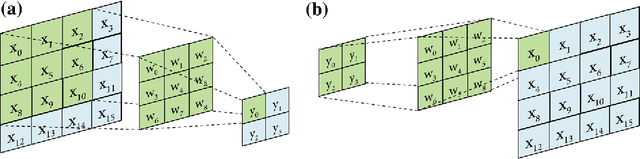
To evaluate the variability of multi-phase flow properties of porous media at the pore scale, it is necessary to acquire a number of representative samples of the void-solid structure. While modern x-ray computer tomography has made it possible to extract three-dimensional images of the pore space, assessment of the variability in the inherent material properties is often experimentally not feasible. We present a novel method to reconstruct the solid-void structure of porous media by applying a generative neural network that allows an implicit description of the probability distribution represented by three-dimensional image datasets. We show, by using an adversarial learning approach for neural networks, that this method of unsupervised learning is able to generate representative samples of porous media that honor their statistics. We successfully compare measures of pore morphology, such as the Euler characteristic, two-point statistics and directional single-phase permeability of synthetic realizations with the calculated properties of a bead pack, Berea sandstone, and Ketton limestone. Results show that GANs can be used to reconstruct high-resolution three-dimensional images of porous media at different scales that are representative of the morphology of the images used to train the neural network. The fully convolutional nature of the trained neural network allows the generation of large samples while maintaining computational efficiency. Compared to classical stochastic methods of image reconstruction, the implicit representation of the learned data distribution can be stored and reused to generate multiple realizations of the pore structure very rapidly.