Stochastic seismic waveform inversion using generative adversarial networks as a geological prior
Paper and Code
Jun 10, 2018
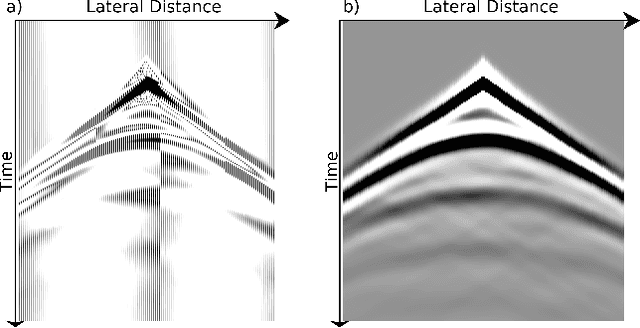
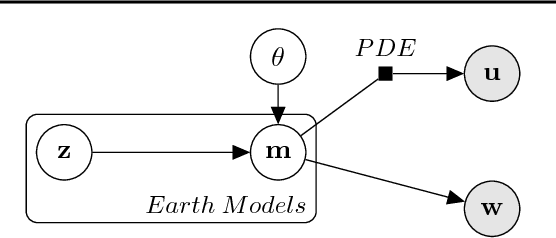

We present an application of deep generative models in the context of partial-differential equation (PDE) constrained inverse problems. We combine a generative adversarial network (GAN) representing an a priori model that creates subsurface geological structures and their petrophysical properties, with the numerical solution of the PDE governing the propagation of acoustic waves within the earth's interior. We perform Bayesian inversion using an approximate Metropolis-adjusted Langevin algorithm (MALA) to sample from the posterior given seismic observations. Gradients with respect to the model parameters governing the forward problem are obtained by solving the adjoint of the acoustic wave equation. Gradients of the mismatch with respect to the latent variables are obtained by leveraging the differentiable nature of the deep neural network used to represent the generative model. We show that approximate MALA sampling allows efficient Bayesian inversion of model parameters obtained from a prior represented by a deep generative model, obtaining a diverse set of realizations that reflect the observed seismic response.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge