DeepFlow: History Matching in the Space of Deep Generative Models
Paper and Code
May 14, 2019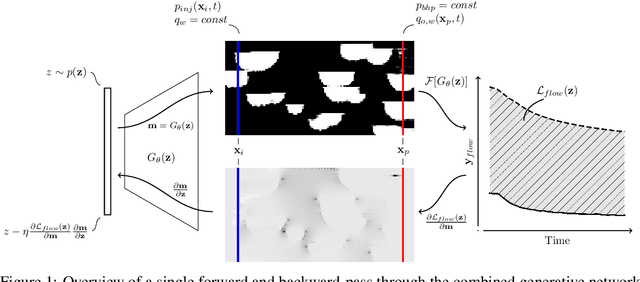



The calibration of a reservoir model with observed transient data of fluid pressures and rates is a key task in obtaining a predictive model of the flow and transport behaviour of the earth's subsurface. The model calibration task, commonly referred to as "history matching", can be formalised as an ill-posed inverse problem where we aim to find the underlying spatial distribution of petrophysical properties that explain the observed dynamic data. We use a generative adversarial network pretrained on geostatistical object-based models to represent the distribution of rock properties for a synthetic model of a hydrocarbon reservoir. The dynamic behaviour of the reservoir fluids is modelled using a transient two-phase incompressible Darcy formulation. We invert for the underlying reservoir properties by first modeling property distributions using the pre-trained generative model then using the adjoint equations of the forward problem to perform gradient descent on the latent variables that control the output of the generative model. In addition to the dynamic observation data, we include well rock-type constraints by introducing an additional objective function. Our contribution shows that for a synthetic test case, we are able to obtain solutions to the inverse problem by optimising in the latent variable space of a deep generative model, given a set of transient observations of a non-linear forward problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge