Neural Networks Asymptotic Behaviours for the Resolution of Inverse Problems

This paper presents a study of the effectiveness of Neural Network (NN) techniques for deconvolution inverse problems relevant for applications in Quantum Field Theory, but also in more general contexts. We consider NN's asymptotic limits, corresponding to Gaussian Processes (GPs), where non-linearities in the parameters of the NN can be neglected. Using these resulting GPs, we address the deconvolution inverse problem in the case of a quantum harmonic oscillator simulated through Monte Carlo techniques on a lattice. In this simple toy model, the results of the inversion can be compared with the known analytical solution. Our findings indicate that solving the inverse problem with a NN yields less performing results than those obtained using the GPs derived from NN's asymptotic limits. Furthermore, we observe the trained NN's accuracy approaching that of GPs with increasing layer width. Notably, one of these GPs defies interpretation as a probabilistic model, offering a novel perspective compared to established methods in the literature. Our results suggest the need for detailed studies of the training dynamics in more realistic set-ups.

Exploring how a Generative AI interprets music

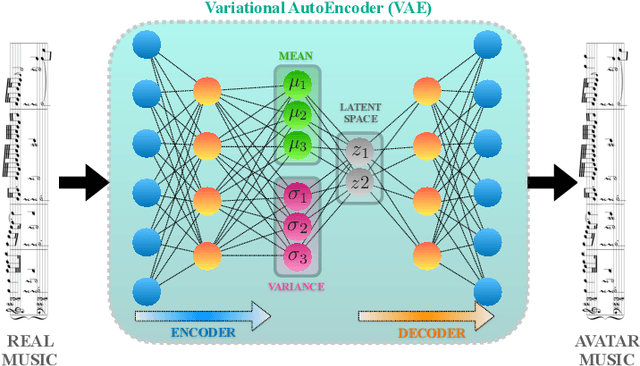
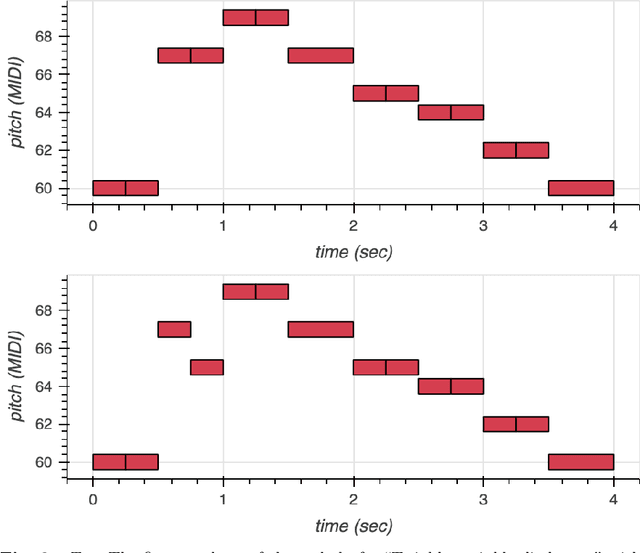
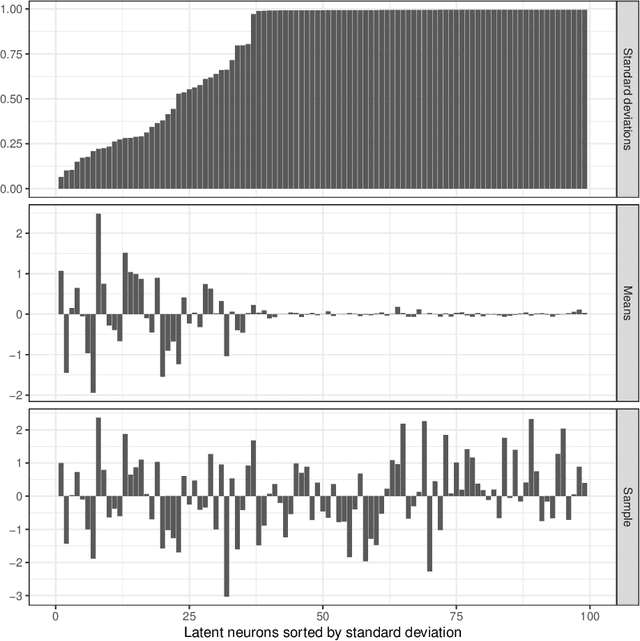
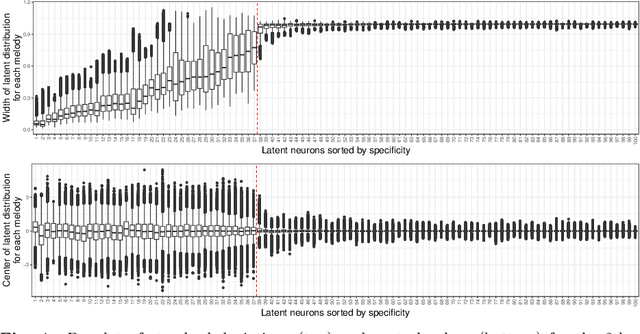
We use Google's MusicVAE, a Variational Auto-Encoder with a 512-dimensional latent space to represent a few bars of music, and organize the latent dimensions according to their relevance in describing music. We find that, on average, most latent neurons remain silent when fed real music tracks: we call these "noise" neurons. The remaining few dozens of latent neurons that do fire are called "music neurons". We ask which neurons carry the musical information and what kind of musical information they encode, namely something that can be identified as pitch, rhythm or melody. We find that most of the information about pitch and rhythm is encoded in the first few music neurons: the neural network has thus constructed a couple of variables that non-linearly encode many human-defined variables used to describe pitch and rhythm. The concept of melody only seems to show up in independent neurons for longer sequences of music.

Machine Learning Trivializing Maps: A First Step Towards Understanding How Flow-Based Samplers Scale Up

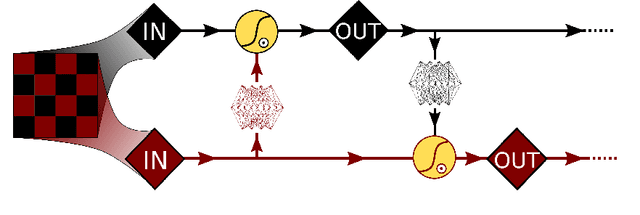
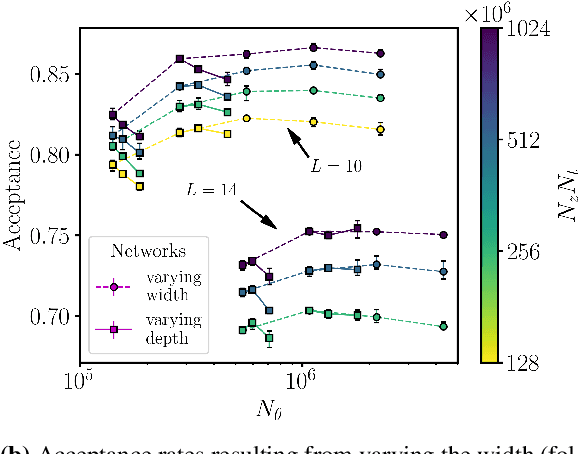
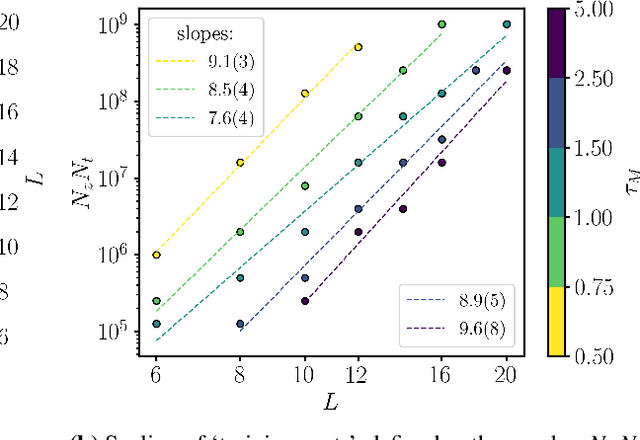
A trivializing map is a field transformation whose Jacobian determinant exactly cancels the interaction terms in the action, providing a representation of the theory in terms of a deterministic transformation of a distribution from which sampling is trivial. Recently, a proof-of-principle study by Albergo, Kanwar and Shanahan [arXiv:1904.12072] demonstrated that approximations of trivializing maps can be `machine-learned' by a class of invertible, differentiable neural models called \textit{normalizing flows}. By ensuring that the Jacobian determinant can be computed efficiently, asymptotically exact sampling from the theory of interest can be performed by drawing samples from a simple distribution and passing them through the network. From a theoretical perspective, this approach has the potential to become more efficient than traditional Markov Chain Monte Carlo sampling techniques, where autocorrelations severely diminish the sampling efficiency as one approaches the continuum limit. A major caveat is that it is not yet understood how the size of models and the cost of training them is expected to scale. As a first step, we have conducted an exploratory scaling study using two-dimensional $\phi^4$ with up to $20^2$ lattice sites. Although the scope of our study is limited to a particular model architecture and training algorithm, initial results paint an interesting picture in which training costs grow very quickly indeed. We describe a candidate explanation for the poor scaling, and outline our intentions to clarify the situation in future work.

Machine learning determination of dynamical parameters: The Ising model case

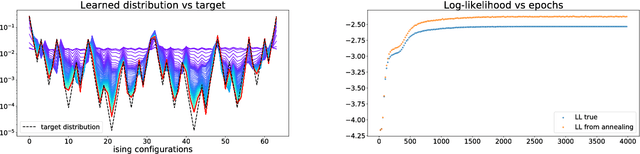
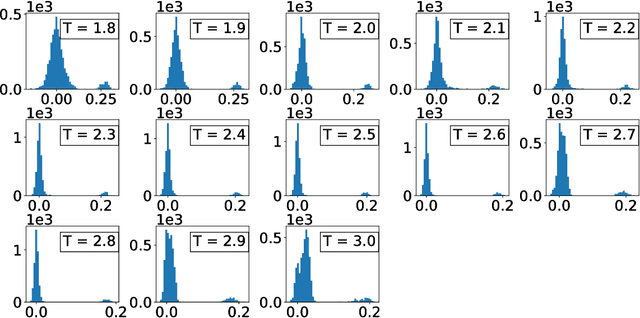
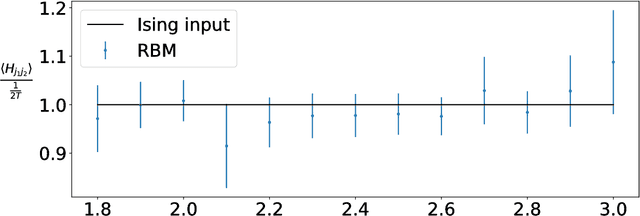
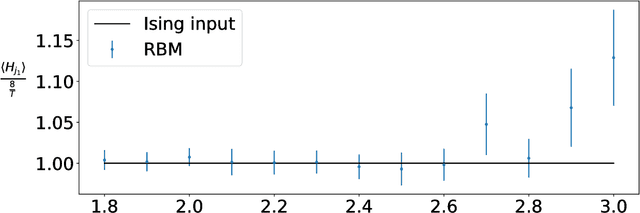
We train a set of Restricted Boltzmann Machines (RBMs) on one- and two-dimensional Ising spin configurations at various values of temperature, generated using Monte Carlo simulations. We validate the training procedure by monitoring several estimators, including measurements of the log-likelihood, with the corresponding partition functions estimated using annealed importance sampling. The effects of various choices of hyper-parameters on training the RBM are discussed in detail, with a generic prescription provided. Finally, we present a closed form expression for extracting the values of couplings, for every $n$-point interaction between the visible nodes of an RBM, in a binary system such as the Ising model. We aim at using this study as the foundation for further investigations of less well-known systems.