Exploring how a Generative AI interprets music

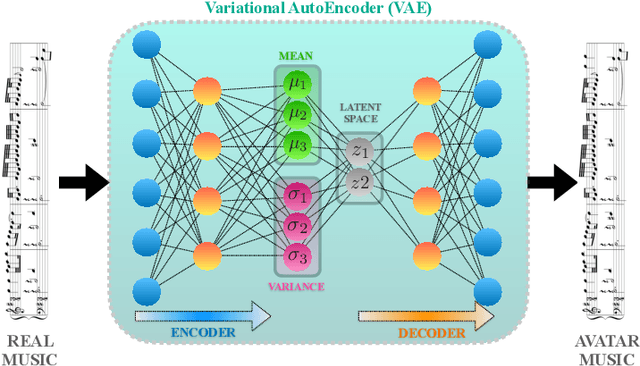
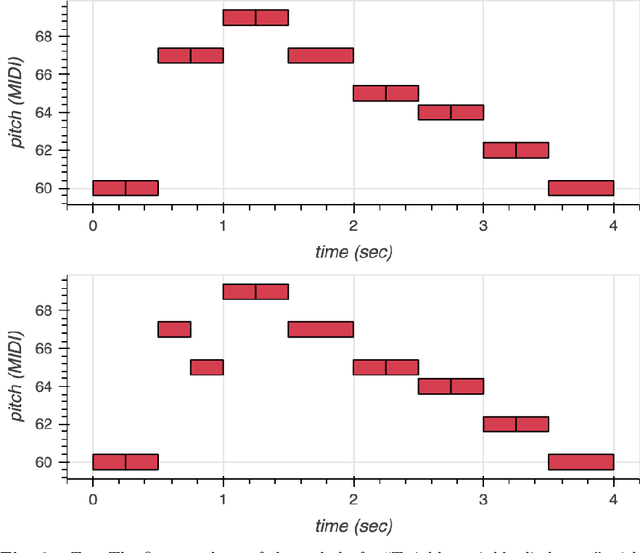
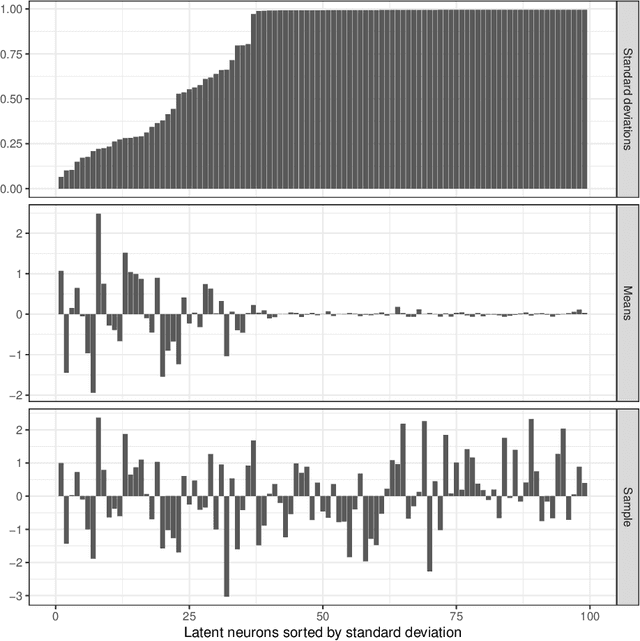
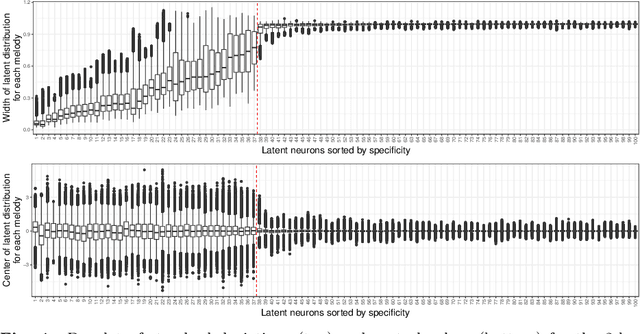
We use Google's MusicVAE, a Variational Auto-Encoder with a 512-dimensional latent space to represent a few bars of music, and organize the latent dimensions according to their relevance in describing music. We find that, on average, most latent neurons remain silent when fed real music tracks: we call these "noise" neurons. The remaining few dozens of latent neurons that do fire are called "music neurons". We ask which neurons carry the musical information and what kind of musical information they encode, namely something that can be identified as pitch, rhythm or melody. We find that most of the information about pitch and rhythm is encoded in the first few music neurons: the neural network has thus constructed a couple of variables that non-linearly encode many human-defined variables used to describe pitch and rhythm. The concept of melody only seems to show up in independent neurons for longer sequences of music.

Symmetry meets AI

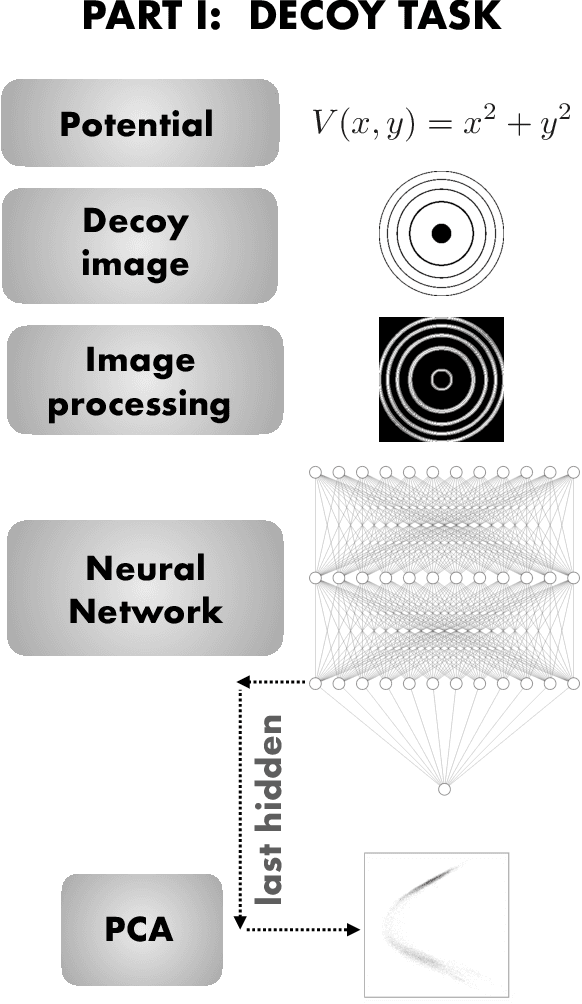
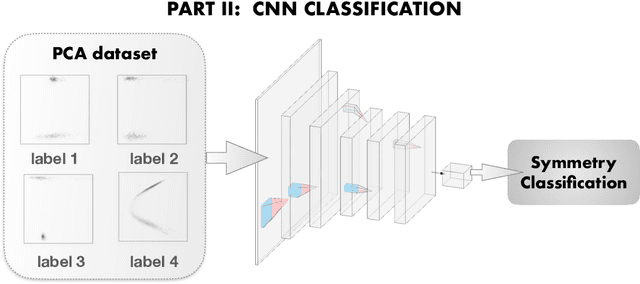
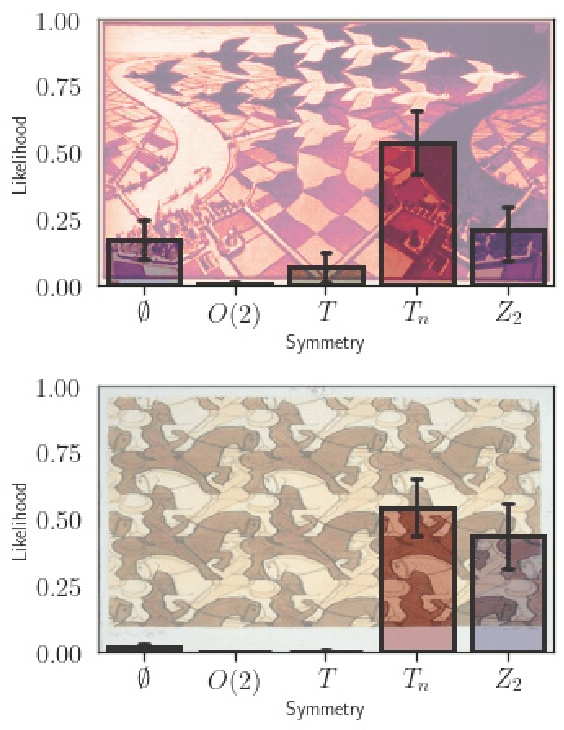
We explore whether Neural Networks (NNs) can {\it discover} the presence of symmetries as they learn to perform a task. For this, we train hundreds of NNs on a {\it decoy task} based on well-controlled Physics templates, where no information on symmetry is provided. We use the output from the last hidden layer of all these NNs, projected to fewer dimensions, as the input for a symmetry classification task, and show that information on symmetry had indeed been identified by the original NN without guidance. As an interdisciplinary application of this procedure, we identify the presence and level of symmetry in artistic paintings from different styles such as those of Picasso, Pollock and Van Gogh.