Machine Learning Trivializing Maps: A First Step Towards Understanding How Flow-Based Samplers Scale Up
Paper and Code
Dec 31, 2021
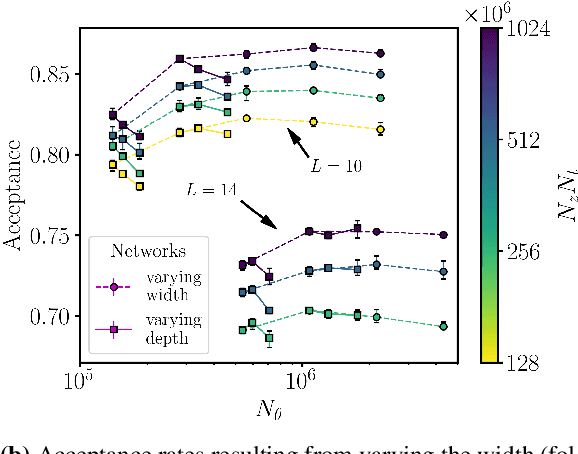
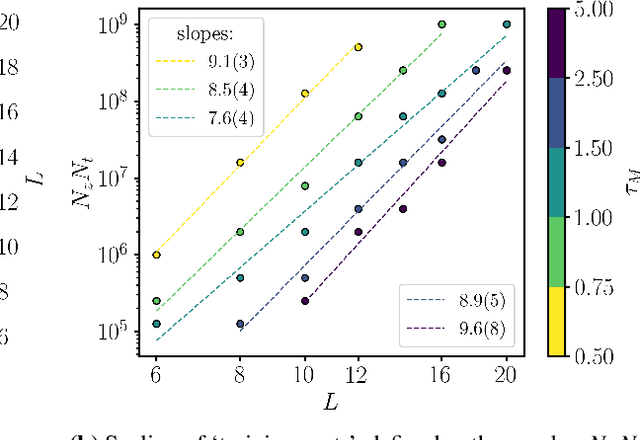
A trivializing map is a field transformation whose Jacobian determinant exactly cancels the interaction terms in the action, providing a representation of the theory in terms of a deterministic transformation of a distribution from which sampling is trivial. Recently, a proof-of-principle study by Albergo, Kanwar and Shanahan [arXiv:1904.12072] demonstrated that approximations of trivializing maps can be `machine-learned' by a class of invertible, differentiable neural models called \textit{normalizing flows}. By ensuring that the Jacobian determinant can be computed efficiently, asymptotically exact sampling from the theory of interest can be performed by drawing samples from a simple distribution and passing them through the network. From a theoretical perspective, this approach has the potential to become more efficient than traditional Markov Chain Monte Carlo sampling techniques, where autocorrelations severely diminish the sampling efficiency as one approaches the continuum limit. A major caveat is that it is not yet understood how the size of models and the cost of training them is expected to scale. As a first step, we have conducted an exploratory scaling study using two-dimensional $\phi^4$ with up to $20^2$ lattice sites. Although the scope of our study is limited to a particular model architecture and training algorithm, initial results paint an interesting picture in which training costs grow very quickly indeed. We describe a candidate explanation for the poor scaling, and outline our intentions to clarify the situation in future work.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge