Towards Neural Sparse Linear Solvers

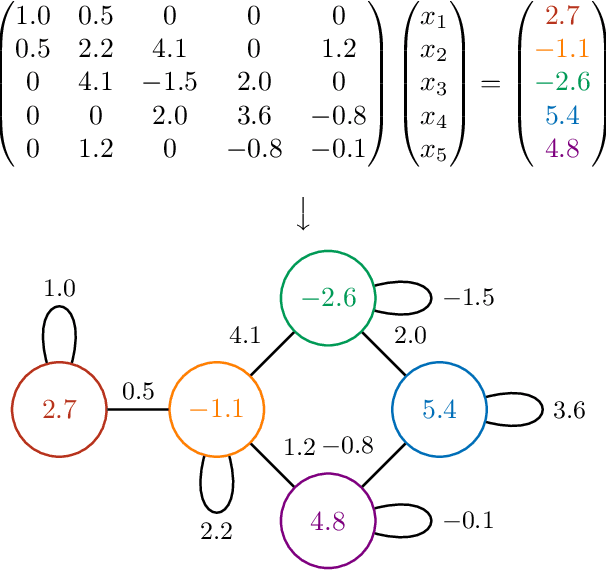
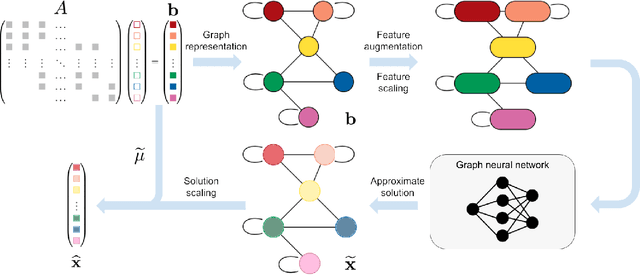
Large sparse symmetric linear systems appear in several branches of science and engineering thanks to the widespread use of the finite element method (FEM). The fastest sparse linear solvers available implement hybrid iterative methods. These methods are based on heuristic algorithms to permute rows and columns or find a preconditioner matrix. In addition, they are inherently sequential, making them unable to leverage the GPU processing power entirely. We propose neural sparse linear solvers, a deep learning framework to learn approximate solvers for sparse symmetric linear systems. Our method relies on representing a sparse symmetric linear system as an undirected weighted graph. Such graph representation is inherently permutation-equivariant and scale-invariant, and it can become the input to a graph neural network trained to regress the solution. We test neural sparse linear solvers on static linear analysis problems from structural engineering. Our method is less accurate than classic algorithms, but it is hardware-independent, fast on GPUs, and applicable to generic sparse symmetric systems without any additional hypothesis. Although many limitations remain, this study shows a general approach to tackle problems involving sparse symmetric matrices using graph neural networks.

StAnD: A Dataset of Linear Static Analysis Problems

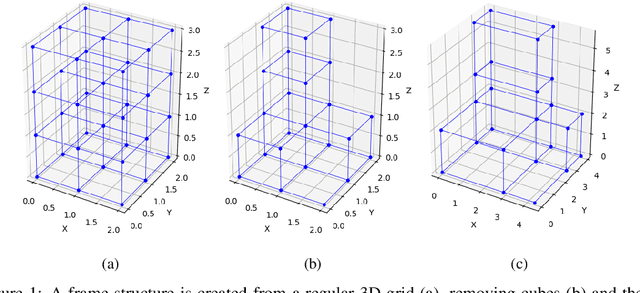
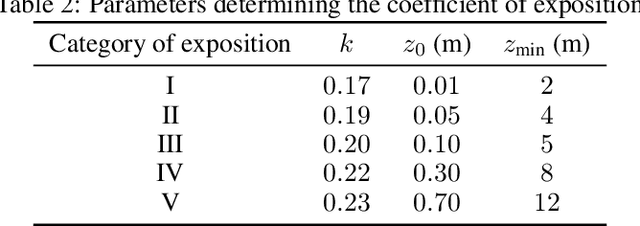
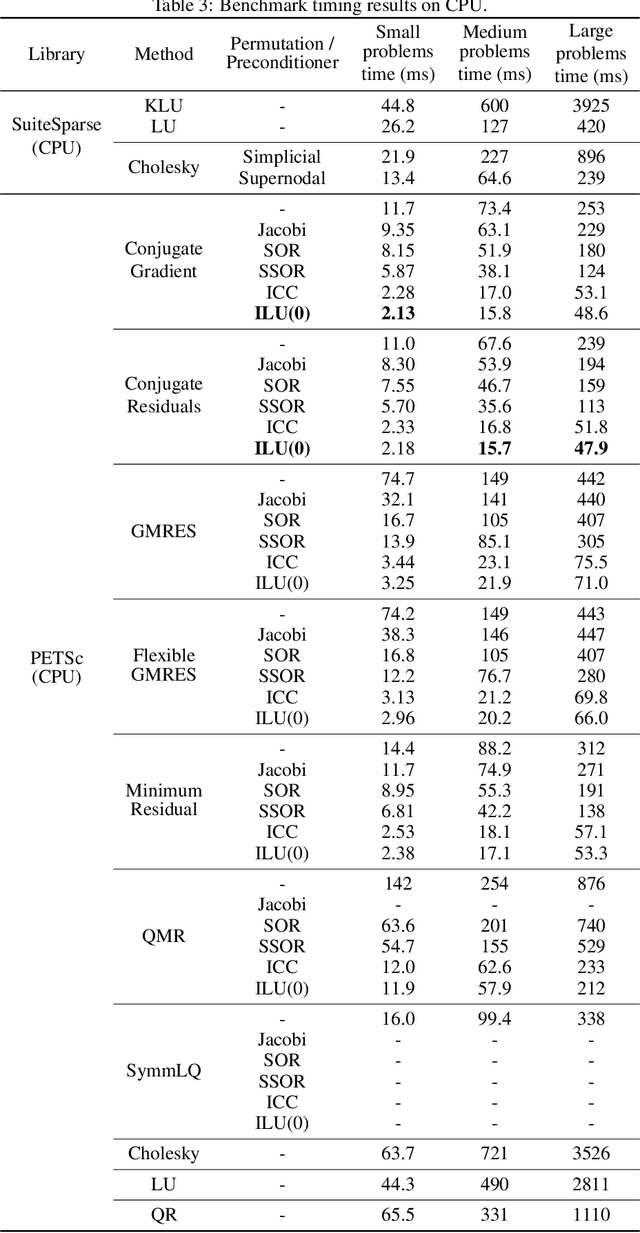
Static analysis of structures is a fundamental step for determining the stability of structures. Both linear and non-linear static analyses consist of the resolution of sparse linear systems obtained by the finite element method. The development of fast and optimized solvers for sparse linear systems appearing in structural engineering requires data to compare existing approaches, tune algorithms or to evaluate new ideas. We introduce the Static Analysis Dataset (StAnD) containing 303.000 static analysis problems obtained applying realistic loads to simulated frame structures. Along with the dataset, we publish a detailed benchmark comparison of the running time of existing solvers both on CPU and GPU. We release the code used to generate the dataset and benchmark existing solvers on Github. To the best of our knowledge, this is the largest dataset for static analysis problems and it is the first public dataset of sparse linear systems (containing both the matrix and a realistic constant term).

Model-centric Data Manifold: the Data Through the Eyes of the Model

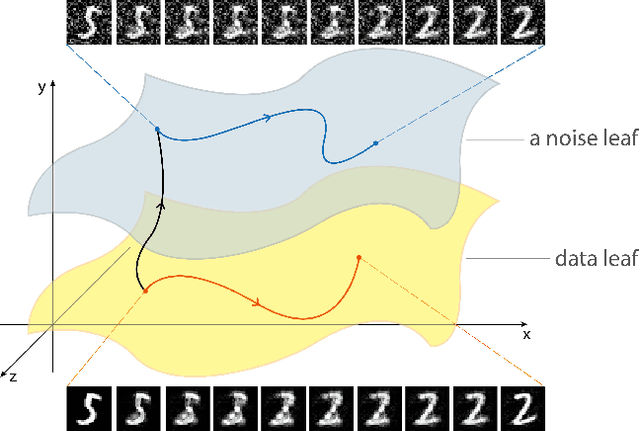
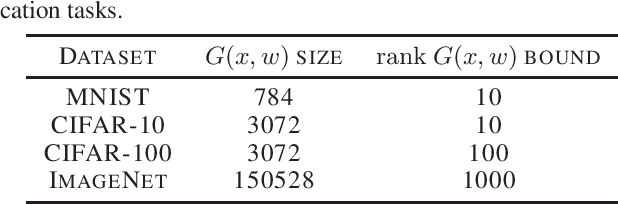
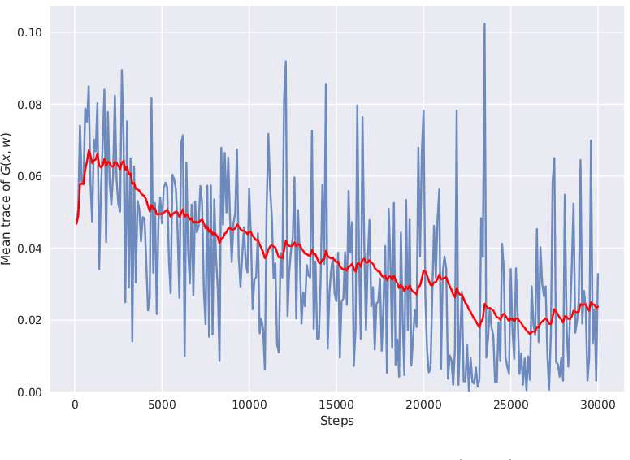
We discover that deep ReLU neural network classifiers can see a low-dimensional Riemannian manifold structure on data. Such structure comes via the local data matrix, a variation of the Fisher information matrix, where the role of the model parameters is taken by the data variables. We obtain a foliation of the data domain and we show that the dataset on which the model is trained lies on a leaf, the data leaf, whose dimension is bounded by the number of classification labels. We validate our results with some experiments with the MNIST dataset: paths on the data leaf connect valid images, while other leaves cover noisy images.