Model-centric Data Manifold: the Data Through the Eyes of the Model
Paper and Code
Apr 26, 2021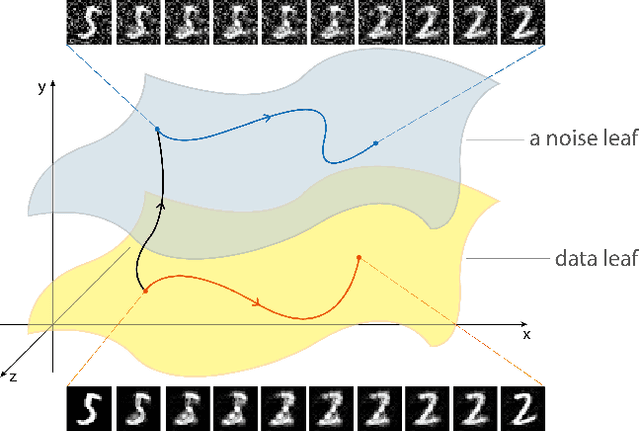
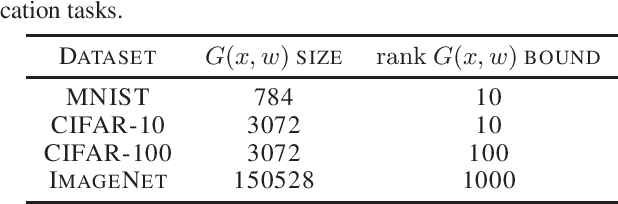
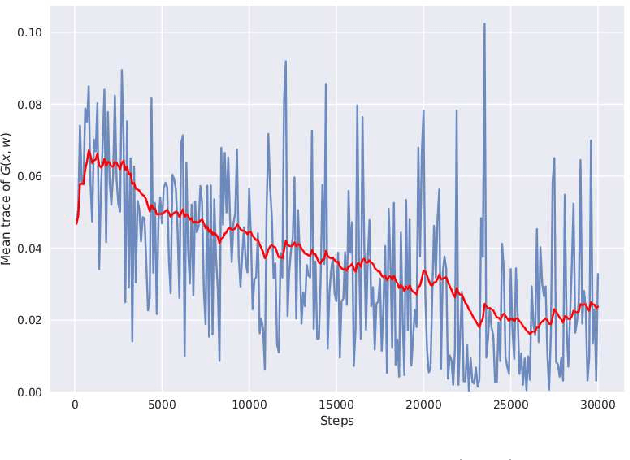

We discover that deep ReLU neural network classifiers can see a low-dimensional Riemannian manifold structure on data. Such structure comes via the local data matrix, a variation of the Fisher information matrix, where the role of the model parameters is taken by the data variables. We obtain a foliation of the data domain and we show that the dataset on which the model is trained lies on a leaf, the data leaf, whose dimension is bounded by the number of classification labels. We validate our results with some experiments with the MNIST dataset: paths on the data leaf connect valid images, while other leaves cover noisy images.
View paper on
 OpenReview
OpenReview
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge