A Marriage between Adversarial Team Games and 2-player Games: Enabling Abstractions, No-regret Learning, and Subgame Solving

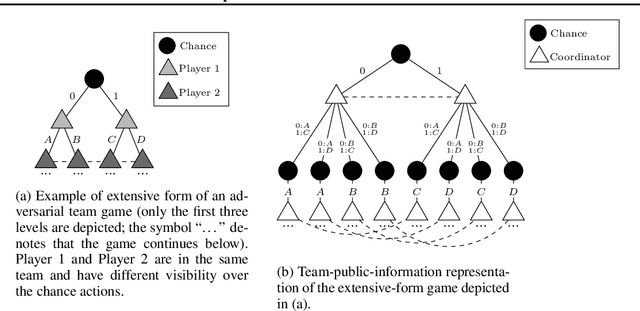
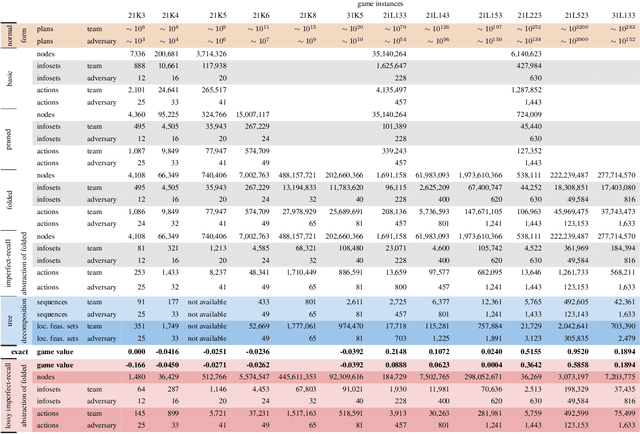
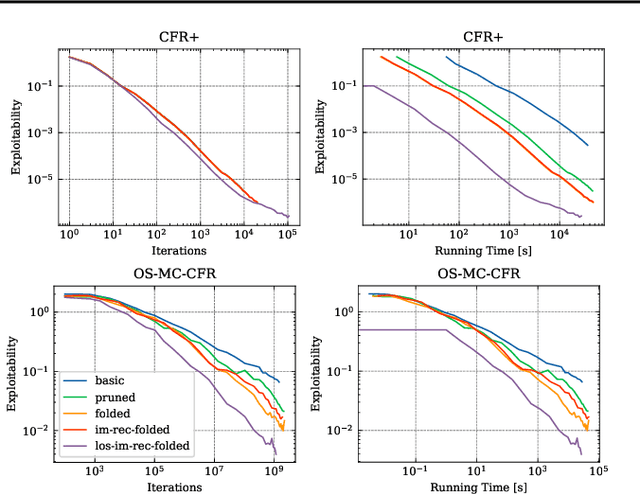
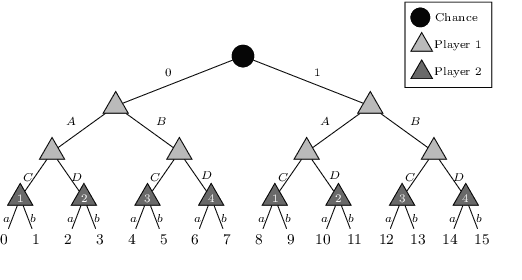
\emph{Ex ante} correlation is becoming the mainstream approach for \emph{sequential adversarial team games}, where a team of players faces another team in a zero-sum game. It is known that team members' asymmetric information makes both equilibrium computation \textsf{APX}-hard and team's strategies not directly representable on the game tree. This latter issue prevents the adoption of successful tools for huge 2-player zero-sum games such as, \emph{e.g.}, abstractions, no-regret learning, and subgame solving. This work shows that we can recover from this weakness by bridging the gap between sequential adversarial team games and 2-player games. In particular, we propose a new, suitable game representation that we call \emph{team-public-information}, in which a team is represented as a single coordinator who only knows information common to the whole team and prescribes to each member an action for any possible private state. The resulting representation is highly \emph{explainable}, being a 2-player tree in which the team's strategies are behavioral with a direct interpretation and more expressive than the original extensive form when designing abstractions. Furthermore, we prove payoff equivalence of our representation, and we provide techniques that, starting directly from the extensive form, generate dramatically more compact representations without information loss. Finally, we experimentally evaluate our techniques when applied to a standard testbed, comparing their performance with the current state of the art.

Public Information Representation for Adversarial Team Games

The peculiarity of adversarial team games resides in the asymmetric information available to the team members during the play, which makes the equilibrium computation problem hard even with zero-sum payoffs. The algorithms available in the literature work with implicit representations of the strategy space and mainly resort to Linear Programming and column generation techniques to enlarge incrementally the strategy space. Such representations prevent the adoption of standard tools such as abstraction generation, game solving, and subgame solving, which demonstrated to be crucial when solving huge, real-world two-player zero-sum games. Differently from these works, we answer the question of whether there is any suitable game representation enabling the adoption of those tools. In particular, our algorithms convert a sequential team game with adversaries to a classical two-player zero-sum game. In this converted game, the team is transformed into a single coordinator player who only knows information common to the whole team and prescribes to the players an action for any possible private state. Interestingly, we show that our game is more expressive than the original extensive-form game as any state/action abstraction of the extensive-form game can be captured by our representation, while the reverse does not hold. Due to the NP-hard nature of the problem, the resulting Public Team game may be exponentially larger than the original one. To limit this explosion, we provide three algorithms, each returning an information-lossless abstraction that dramatically reduces the size of the tree. These abstractions can be produced without generating the original game tree. Finally, we show the effectiveness of the proposed approach by presenting experimental results on Kuhn and Leduc Poker games, obtained by applying state-of-art algorithms for two-player zero-sum games on the converted games