A Marriage between Adversarial Team Games and 2-player Games: Enabling Abstractions, No-regret Learning, and Subgame Solving
Paper and Code
Jun 18, 2022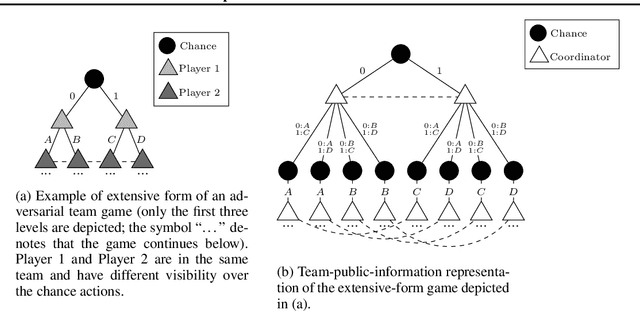
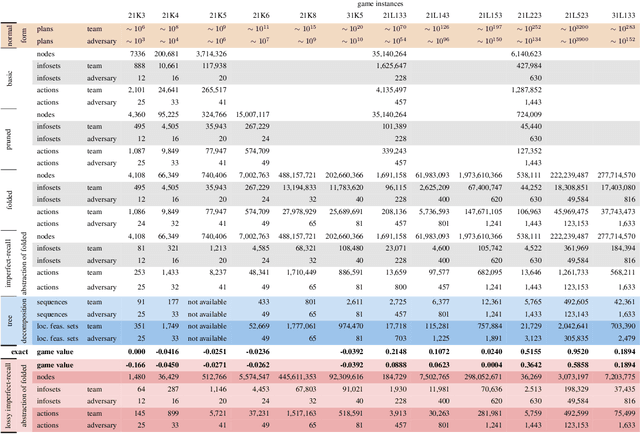
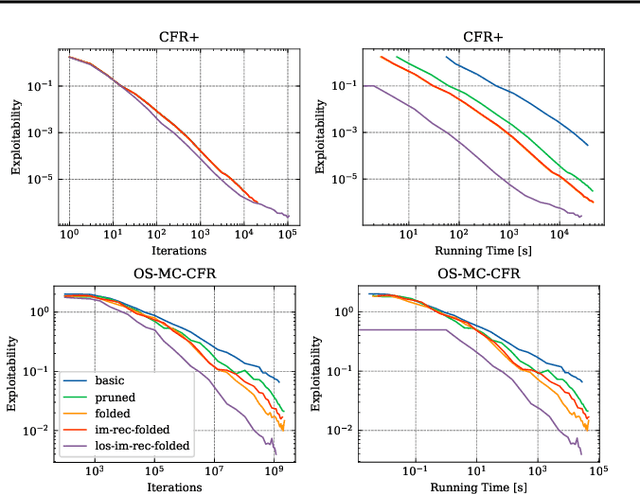
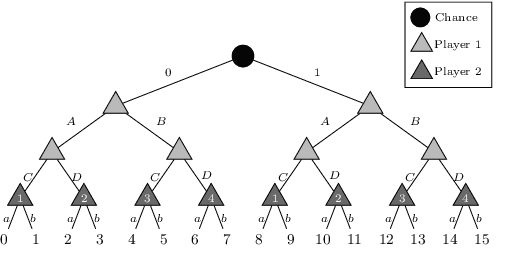
\emph{Ex ante} correlation is becoming the mainstream approach for \emph{sequential adversarial team games}, where a team of players faces another team in a zero-sum game. It is known that team members' asymmetric information makes both equilibrium computation \textsf{APX}-hard and team's strategies not directly representable on the game tree. This latter issue prevents the adoption of successful tools for huge 2-player zero-sum games such as, \emph{e.g.}, abstractions, no-regret learning, and subgame solving. This work shows that we can recover from this weakness by bridging the gap between sequential adversarial team games and 2-player games. In particular, we propose a new, suitable game representation that we call \emph{team-public-information}, in which a team is represented as a single coordinator who only knows information common to the whole team and prescribes to each member an action for any possible private state. The resulting representation is highly \emph{explainable}, being a 2-player tree in which the team's strategies are behavioral with a direct interpretation and more expressive than the original extensive form when designing abstractions. Furthermore, we prove payoff equivalence of our representation, and we provide techniques that, starting directly from the extensive form, generate dramatically more compact representations without information loss. Finally, we experimentally evaluate our techniques when applied to a standard testbed, comparing their performance with the current state of the art.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge