A State-Space Perspective on Modelling and Inference for Online Skill Rating

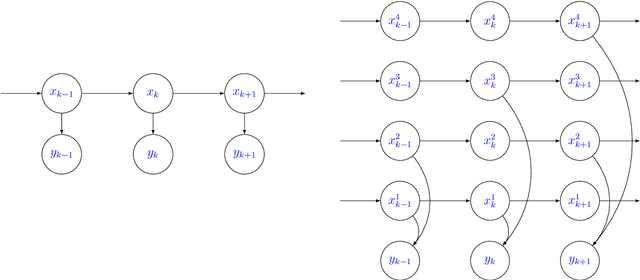
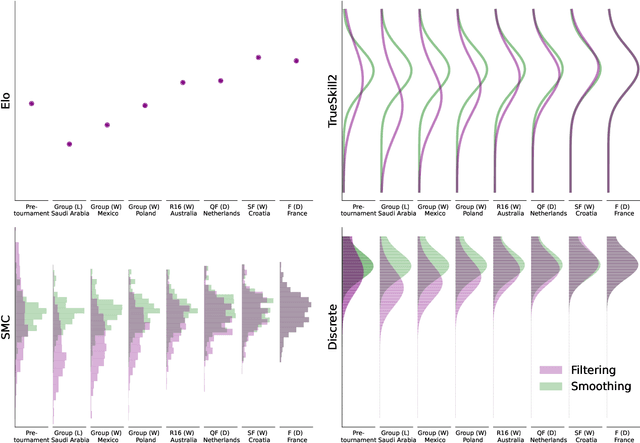
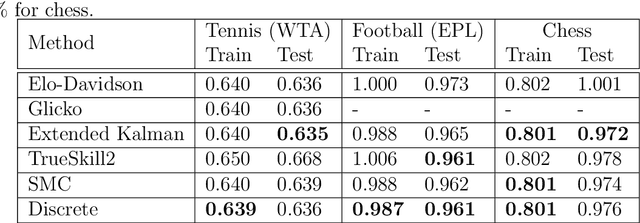
This paper offers a comprehensive review of the main methodologies used for skill rating in competitive sports. We advocate for a state-space model perspective, wherein players' skills are represented as time-varying, and match results serve as the sole observed quantities. The state-space model perspective facilitates the decoupling of modeling and inference, enabling a more focused approach highlighting model assumptions, while also fostering the development of general-purpose inference tools. We explore the essential steps involved in constructing a state-space model for skill rating before turning to a discussion on the three stages of inference: filtering, smoothing and parameter estimation. Throughout, we examine the computational challenges of scaling up to high-dimensional scenarios involving numerous players and matches, highlighting approximations and reductions used to address these challenges effectively. We provide concise summaries of popular methods documented in the literature, along with their inferential paradigms and introduce new approaches to skill rating inference based on sequential Monte Carlo and finite state-spaces. We close with numerical experiments demonstrating a practical workflow on real data across different sports.

Consistent and fast inference in compartmental models of epidemics using Poisson Approximate Likelihoods

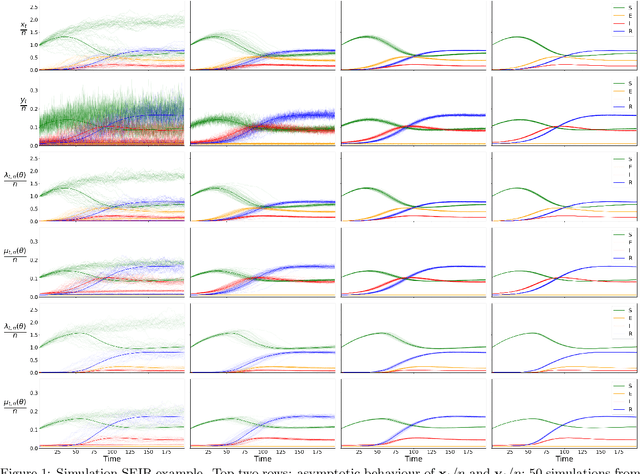
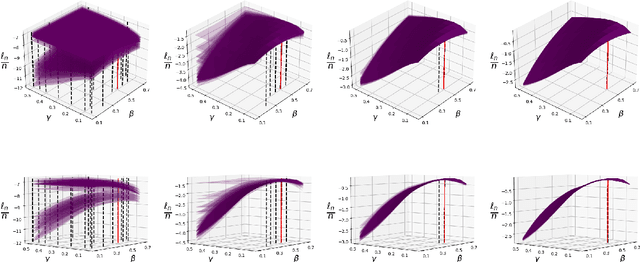
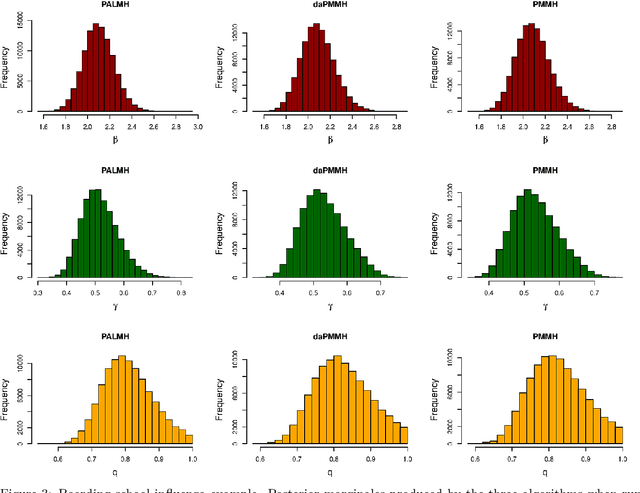
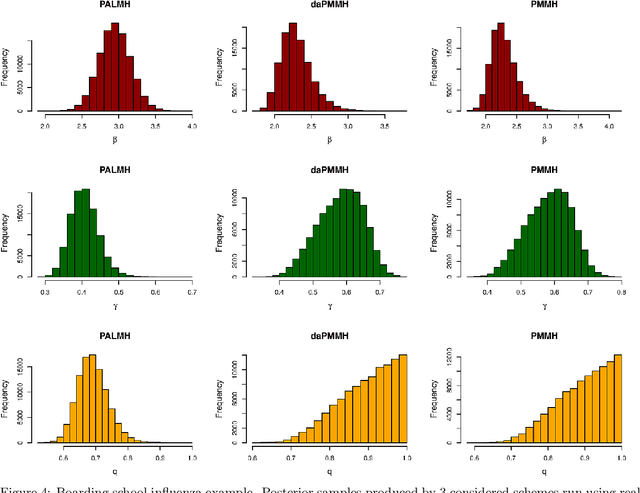
Addressing the challenge of scaling-up epidemiological inference to complex and heterogeneous models, we introduce Poisson Approximate Likelihood (PAL) methods. In contrast to the popular ODE approach to compartmental modelling, in which a large population limit is used to motivate a deterministic model, PALs are derived from approximate filtering equations for finite-population, stochastic compartmental models, and the large population limit drives the consistency of maximum PAL estimators. Our theoretical results appear to be the first likelihood-based parameter estimation consistency results applicable across a broad class of partially observed stochastic compartmental models. Compared to simulation-based methods such as Approximate Bayesian Computation and Sequential Monte Carlo, PALs are simple to implement, involving only elementary arithmetic operations and no tuning parameters; and fast to evaluate, requiring no simulation from the model and having computational cost independent of population size. Through examples, we demonstrate how PALs can be: embedded within Delayed Acceptance Particle Markov Chain Monte Carlo to facilitate Bayesian inference; used to fit an age-structured model of influenza, taking advantage of automatic differentiation in Stan; and applied to calibrate a spatial meta-population model of measles.

Inference in Stochastic Epidemic Models via Multinomial Approximations

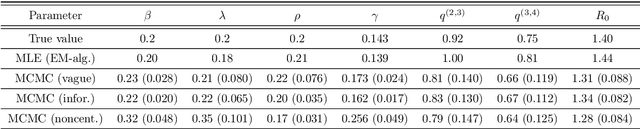
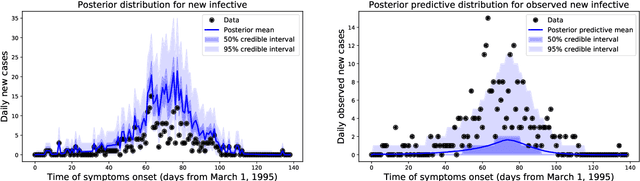
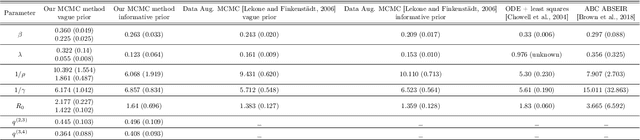
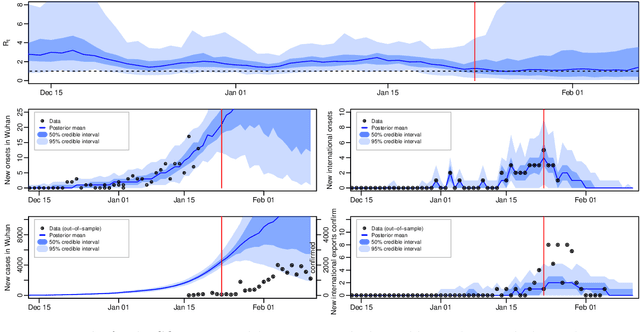
We introduce a new method for inference in stochastic epidemic models which uses recursive multinomial approximations to integrate over unobserved variables and thus circumvent likelihood intractability. The method is applicable to a class of discrete-time, finite-population compartmental models with partial, randomly under-reported or missing count observations. In contrast to state-of-the-art alternatives such as Approximate Bayesian Computation techniques, no forward simulation of the model is required and there are no tuning parameters. Evaluating the approximate marginal likelihood of model parameters is achieved through a computationally simple filtering recursion. The accuracy of the approximation is demonstrated through analysis of real and simulated data using a model of the 1995 Ebola outbreak in the Democratic Republic of Congo. We show how the method can be embedded within a Sequential Monte Carlo approach to estimating the time-varying reproduction number of COVID-19 in Wuhan, China, recently published by Kucharski et al. 2020.

Dynamic Bayesian Neural Networks

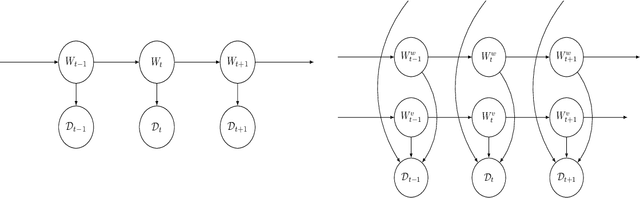
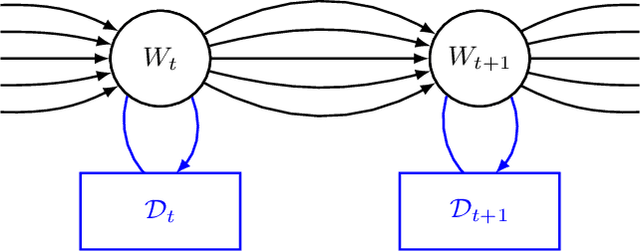
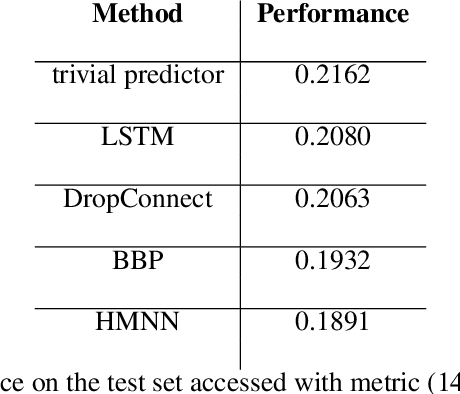
We define an evolving in time Bayesian neural network called a Hidden Markov neural network. The weights of the feed-forward neural network are modelled with the hidden states of a Hidden Markov model, the whose observed process is given by the available data. A filtering algorithm is used to learn a variational approximation to the evolving in time posterior over the weights. Training is pursued through a sequential version of Bayes by Backprop, which is enriched with a stronger regularization technique called variational DropConnect. The experiments are focused on streaming data and time series. On the one hand, we train on MNIST when only a portion of the dataset is available at a time. On the other hand, we perform frames prediction on a waving flag video.

Exploiting locality in high-dimensional factorial hidden Markov models

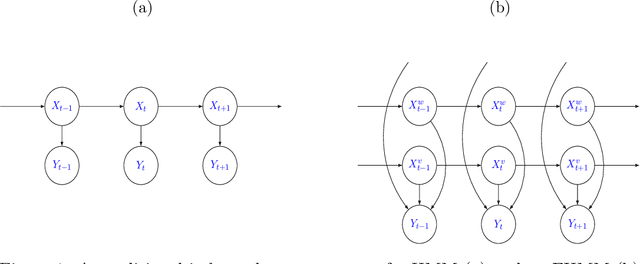
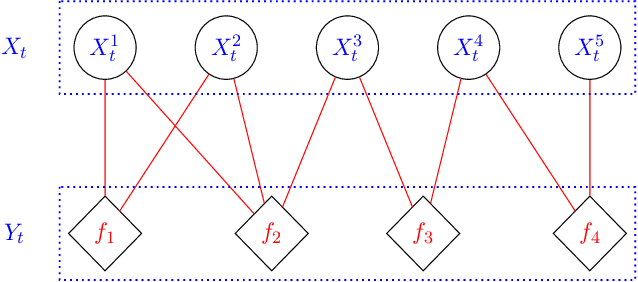
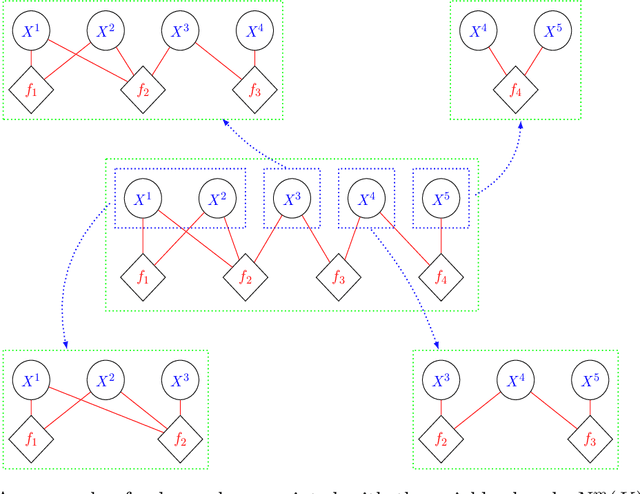
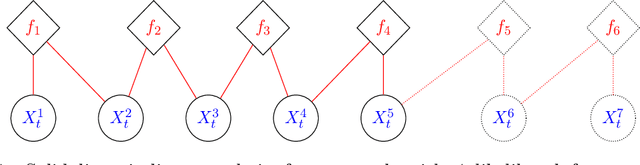
We propose algorithms for approximate filtering and smoothing in high-dimensional factorial hidden Markov models. The approximation involves discarding, in a principled way, likelihood factors according a notion of locality in a factor graph associated with the emission distribution. This allows the exponential-in-dimension cost of exact filtering and smoothing to be avoided. We prove that the approximation accuracy, measured in a local total variation norm, is `dimension-free' in the sense that as the overall dimension of the model increases the error bounds we derive do not necessarily degrade. A key step in the analysis is to quantify the error introduced by localizing the likelihood function in a Bayes' rule update. The factorial structure of the likelihood function which we exploit arises naturally when data have known spatial or network structure. We demonstrate the new algorithms on synthetic examples and a London Underground passenger flow problem, where the factor graph is effectively given by the train network.