Consistent and fast inference in compartmental models of epidemics using Poisson Approximate Likelihoods

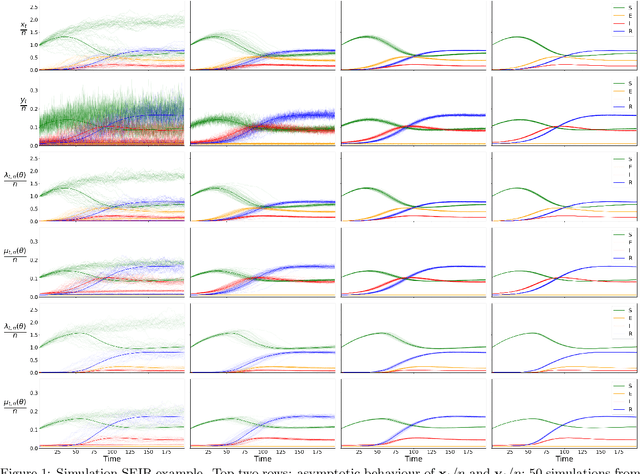
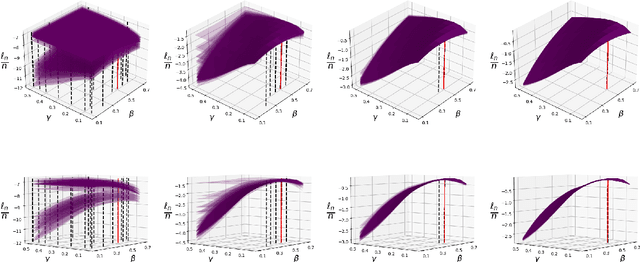
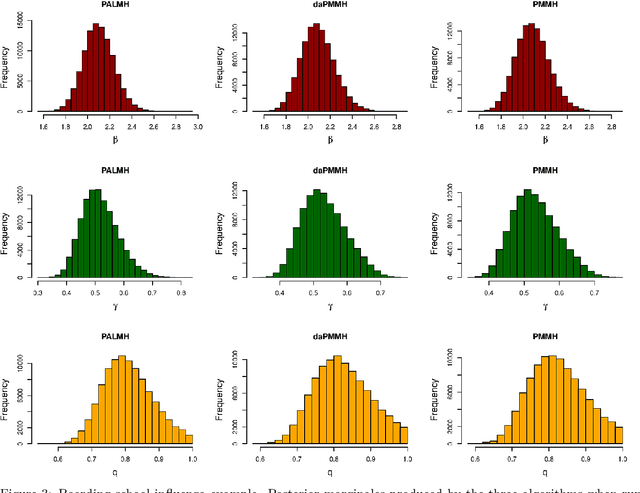
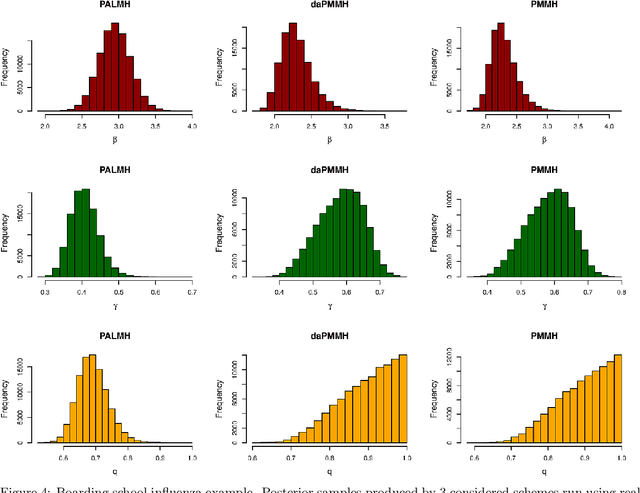
Addressing the challenge of scaling-up epidemiological inference to complex and heterogeneous models, we introduce Poisson Approximate Likelihood (PAL) methods. In contrast to the popular ODE approach to compartmental modelling, in which a large population limit is used to motivate a deterministic model, PALs are derived from approximate filtering equations for finite-population, stochastic compartmental models, and the large population limit drives the consistency of maximum PAL estimators. Our theoretical results appear to be the first likelihood-based parameter estimation consistency results applicable across a broad class of partially observed stochastic compartmental models. Compared to simulation-based methods such as Approximate Bayesian Computation and Sequential Monte Carlo, PALs are simple to implement, involving only elementary arithmetic operations and no tuning parameters; and fast to evaluate, requiring no simulation from the model and having computational cost independent of population size. Through examples, we demonstrate how PALs can be: embedded within Delayed Acceptance Particle Markov Chain Monte Carlo to facilitate Bayesian inference; used to fit an age-structured model of influenza, taking advantage of automatic differentiation in Stan; and applied to calibrate a spatial meta-population model of measles.