A Simultaneous Approach for Training Neural Differential-Algebraic Systems of Equations

Scientific machine learning is an emerging field that broadly describes the combination of scientific computing and machine learning to address challenges in science and engineering. Within the context of differential equations, this has produced highly influential methods, such as neural ordinary differential equations (NODEs). Recent works extend this line of research to consider neural differential-algebraic systems of equations (DAEs), where some unknown relationships within the DAE are learned from data. Training neural DAEs, similarly to neural ODEs, is computationally expensive, as it requires the solution of a DAE for every parameter update. Further, the rigorous consideration of algebraic constraints is difficult within common deep learning training algorithms such as stochastic gradient descent. In this work, we apply the simultaneous approach to neural DAE problems, resulting in a fully discretized nonlinear optimization problem, which is solved to local optimality and simultaneously obtains the neural network parameters and the solution to the corresponding DAE. We extend recent work demonstrating the simultaneous approach for neural ODEs, by presenting a general framework to solve neural DAEs, with explicit consideration of hybrid models, where some components of the DAE are known, e.g. physics-informed constraints. Furthermore, we present a general strategy for improving the performance and convergence of the nonlinear programming solver, based on solving an auxiliary problem for initialization and approximating Hessian terms. We achieve promising results in terms of accuracy, model generalizability and computational cost, across different problem settings such as sparse data, unobserved states and multiple trajectories. Lastly, we provide several promising future directions to improve the scalability and robustness of our approach.

Conflict-Based Model Predictive Control for Scalable Multi-Robot Motion Planning

This paper presents a scalable multi-robot motion planning algorithm called Conflict-Based Model Predictive Control (CB-MPC). Inspired by Conflict-Based Search (CBS), the planner leverages a similar high-level conflict tree to efficiently resolve robot-robot conflicts in the continuous space, while reasoning about each agent's kinematic and dynamic constraints and actuation limits using MPC as the low-level planner. We show that tracking high-level multi-robot plans with a vanilla MPC controller is insufficient, and results in unexpected collisions in tight navigation scenarios. Compared to other variations of multi-robot MPC like joint, prioritized, and distributed, we demonstrate that CB-MPC improves the executability and success rate, allows for closer robot-robot interactions, and reduces the computational cost significantly without compromising the solution quality across a variety of environments. Furthermore, we show that CB-MPC combined with a high-level path planner can effectively substitute computationally expensive full-horizon multi-robot kinodynamic planners.

Contact-Implicit Trajectory Optimization using Orthogonal Collocation

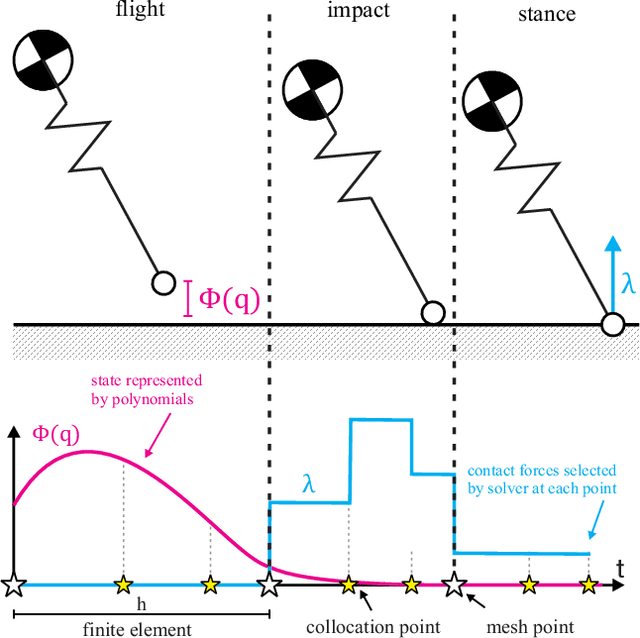
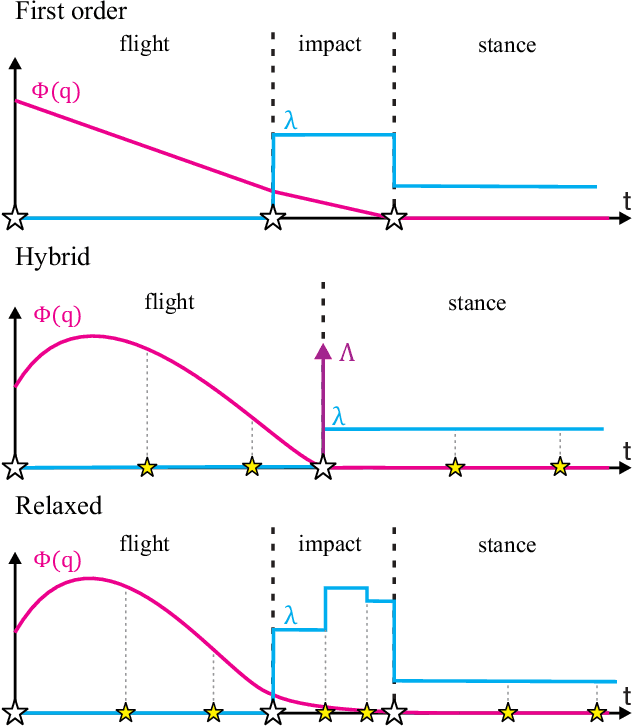
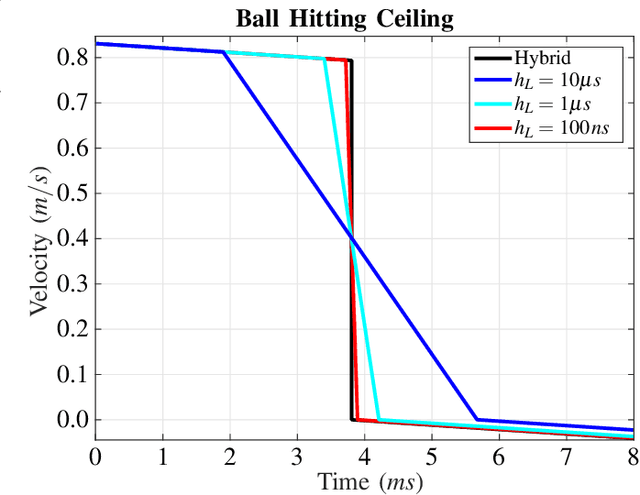
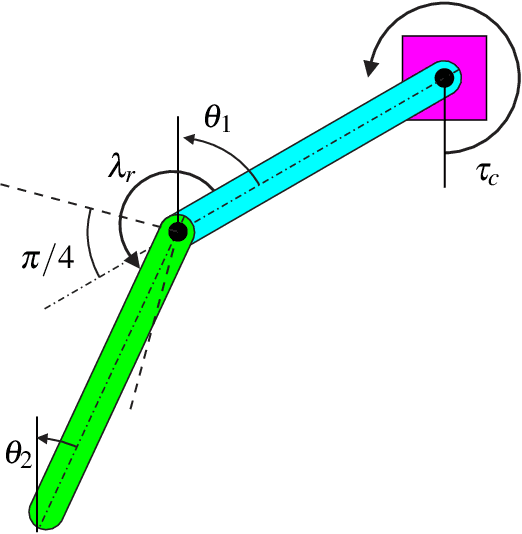
In this paper we propose a method to improve the accuracy of trajectory optimization for dynamic robots with intermittent contact by using orthogonal collocation. Until recently, most trajectory optimization methods for systems with contacts employ mode-scheduling, which requires an a priori knowledge of the contact order and thus cannot produce complex or non-intuitive behaviors. Contact-implicit trajectory optimization methods offer a solution to this by allowing the optimization to make or break contacts as needed, but thus far have suffered from poor accuracy. Here, we combine methods from direct collocation using higher order orthogonal polynomials with contact-implicit optimization to generate trajectories with significantly improved accuracy. The key insight is to increase the order of the polynomial representation while maintaining the assumption that impact occurs over the duration of one finite element.