Fully Bayesian Logistic Regression with Hyper-Lasso Priors for High-dimensional Feature Selection

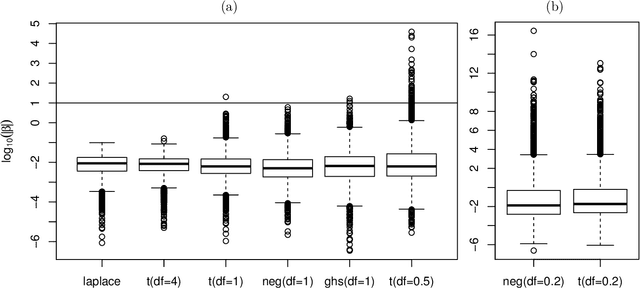
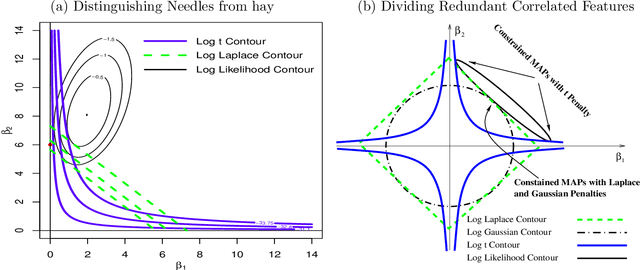
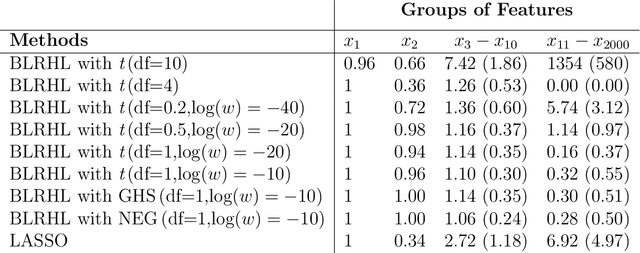
High-dimensional feature selection arises in many areas of modern science. For example, in genomic research we want to find the genes that can be used to separate tissues of different classes (e.g. cancer and normal) from tens of thousands of genes that are active (expressed) in certain tissue cells. To this end, we wish to fit regression and classification models with a large number of features (also called variables, predictors). In the past decade, penalized likelihood methods for fitting regression models based on hyper-LASSO penalization have received increasing attention in the literature. However, fully Bayesian methods that use Markov chain Monte Carlo (MCMC) are still in lack of development in the literature. In this paper we introduce an MCMC (fully Bayesian) method for learning severely multi-modal posteriors of logistic regression models based on hyper-LASSO priors (non-convex penalties). Our MCMC algorithm uses Hamiltonian Monte Carlo in a restricted Gibbs sampling framework; we call our method Bayesian logistic regression with hyper-LASSO (BLRHL) priors. We have used simulation studies and real data analysis to demonstrate the superior performance of hyper-LASSO priors, and to investigate the issues of choosing heaviness and scale of hyper-LASSO priors.

A Method for Compressing Parameters in Bayesian Models with Application to Logistic Sequence Prediction Models

Bayesian classification and regression with high order interactions is largely infeasible because Markov chain Monte Carlo (MCMC) would need to be applied with a great many parameters, whose number increases rapidly with the order. In this paper we show how to make it feasible by effectively reducing the number of parameters, exploiting the fact that many interactions have the same values for all training cases. Our method uses a single ``compressed'' parameter to represent the sum of all parameters associated with a set of patterns that have the same value for all training cases. Using symmetric stable distributions as the priors of the original parameters, we can easily find the priors of these compressed parameters. We therefore need to deal only with a much smaller number of compressed parameters when training the model with MCMC. The number of compressed parameters may have converged before considering the highest possible order. After training the model, we can split these compressed parameters into the original ones as needed to make predictions for test cases. We show in detail how to compress parameters for logistic sequence prediction models. Experiments on both simulated and real data demonstrate that a huge number of parameters can indeed be reduced by our compression method.

Bayesian Classification and Regression with High Dimensional Features

This thesis responds to the challenges of using a large number, such as thousands, of features in regression and classification problems. There are two situations where such high dimensional features arise. One is when high dimensional measurements are available, for example, gene expression data produced by microarray techniques. For computational or other reasons, people may select only a small subset of features when modelling such data, by looking at how relevant the features are to predicting the response, based on some measure such as correlation with the response in the training data. Although it is used very commonly, this procedure will make the response appear more predictable than it actually is. In Chapter 2, we propose a Bayesian method to avoid this selection bias, with application to naive Bayes models and mixture models. High dimensional features also arise when we consider high-order interactions. The number of parameters will increase exponentially with the order considered. In Chapter 3, we propose a method for compressing a group of parameters into a single one, by exploiting the fact that many predictor variables derived from high-order interactions have the same values for all the training cases. The number of compressed parameters may have converged before considering the highest possible order. We apply this compression method to logistic sequence prediction models and logistic classification models. We use both simulated data and real data to test our methods in both chapters.