Fully Bayesian Logistic Regression with Hyper-Lasso Priors for High-dimensional Feature Selection
Paper and Code
May 12, 2018
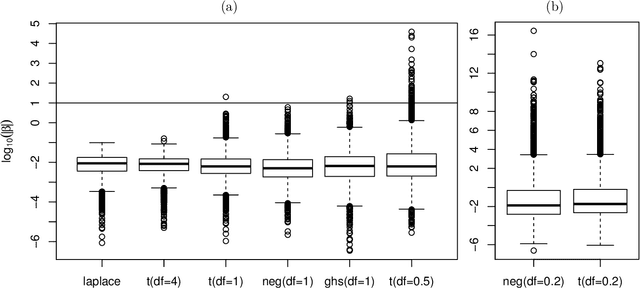
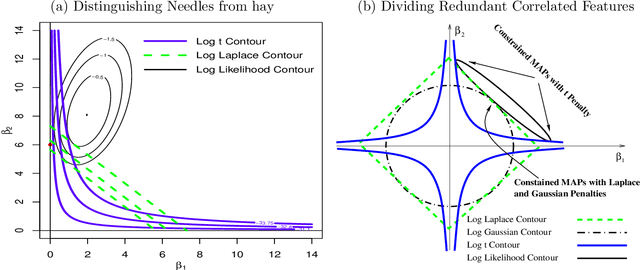
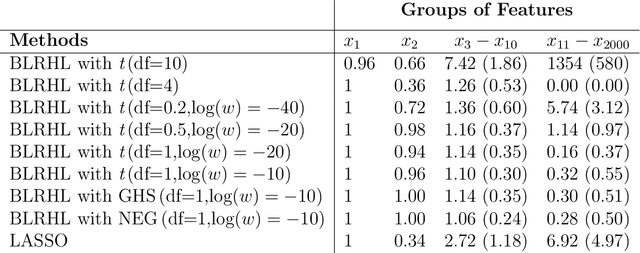
High-dimensional feature selection arises in many areas of modern science. For example, in genomic research we want to find the genes that can be used to separate tissues of different classes (e.g. cancer and normal) from tens of thousands of genes that are active (expressed) in certain tissue cells. To this end, we wish to fit regression and classification models with a large number of features (also called variables, predictors). In the past decade, penalized likelihood methods for fitting regression models based on hyper-LASSO penalization have received increasing attention in the literature. However, fully Bayesian methods that use Markov chain Monte Carlo (MCMC) are still in lack of development in the literature. In this paper we introduce an MCMC (fully Bayesian) method for learning severely multi-modal posteriors of logistic regression models based on hyper-LASSO priors (non-convex penalties). Our MCMC algorithm uses Hamiltonian Monte Carlo in a restricted Gibbs sampling framework; we call our method Bayesian logistic regression with hyper-LASSO (BLRHL) priors. We have used simulation studies and real data analysis to demonstrate the superior performance of hyper-LASSO priors, and to investigate the issues of choosing heaviness and scale of hyper-LASSO priors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge