Loic A. Royer
Image Deconvolution via Noise-Tolerant Self-Supervised Inversion
Jun 11, 2020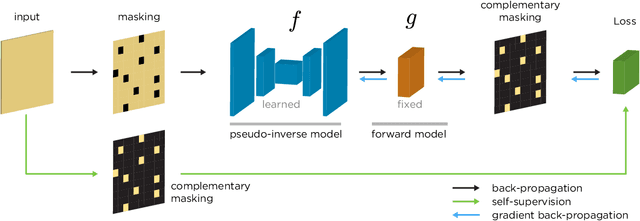
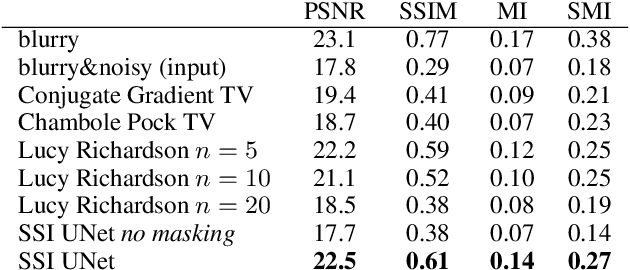
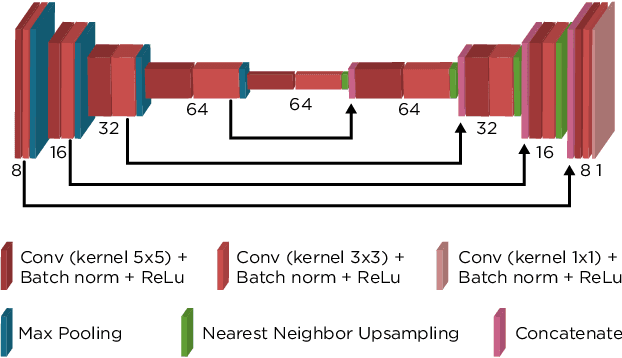

Abstract:We propose a general framework for solving inverse problems in the presence of noise that requires no signal prior, no noise estimate, and no clean training data. We only require that the forward model be available and that the noise be statistically independent across measurement dimensions. We build upon the theory of $\mathcal{J}$-invariant functions (Batson & Royer 2019, arXiv:1901.11365) and show how self-supervised denoising \emph{\`a la} Noise2Self is a special case of learning a noise-tolerant pseudo-inverse of the identity. We demonstrate our approach by showing how a convolutional neural network can be taught in a self-supervised manner to deconvolve images and surpass in image quality classical inversion schemes such as Lucy-Richardson deconvolution.
Convexity Shape Constraints for Image Segmentation
Sep 07, 2015



Abstract:Segmenting an image into multiple components is a central task in computer vision. In many practical scenarios, prior knowledge about plausible components is available. Incorporating such prior knowledge into models and algorithms for image segmentation is highly desirable, yet can be non-trivial. In this work, we introduce a new approach that allows, for the first time, to constrain some or all components of a segmentation to have convex shapes. Specifically, we extend the Minimum Cost Multicut Problem by a class of constraints that enforce convexity. To solve instances of this APX-hard integer linear program to optimality, we separate the proposed constraints in the branch-and-cut loop of a state-of-the-art ILP solver. Results on natural and biological images demonstrate the effectiveness of the approach as well as its advantage over the state-of-the-art heuristic.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge