Liyang Hu
A Parameter-free Nonconvex Low-rank Tensor Completion Model for Spatiotemporal Traffic Data Recovery
Sep 28, 2022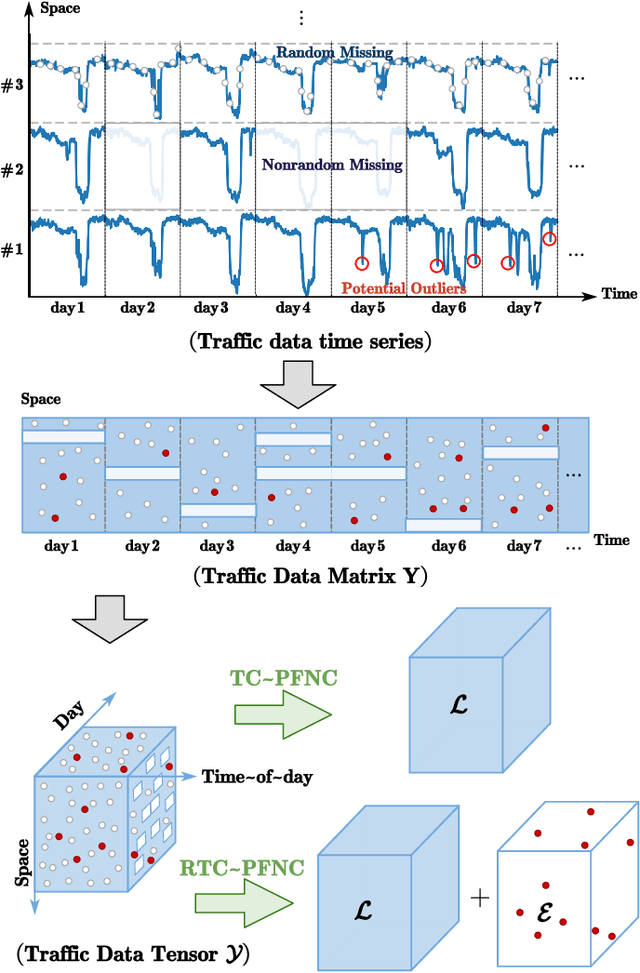

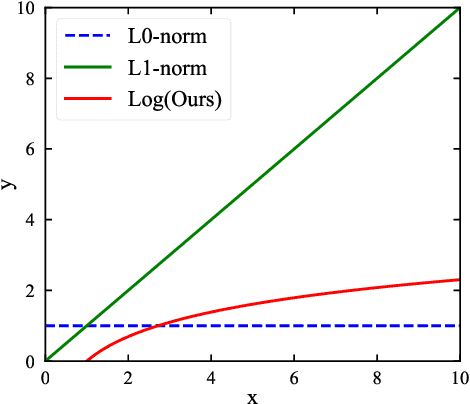

Abstract:Traffic data chronically suffer from missing and corruption, leading to accuracy and utility reduction in subsequent Intelligent Transportation System (ITS) applications. Noticing the inherent low-rank property of traffic data, numerous studies formulated missing traffic data recovery as a low-rank tensor completion (LRTC) problem. Due to the non-convexity and discreteness of the rank minimization in LRTC, existing methods either replaced rank with convex surrogates that are quite far away from the rank function or approximated rank with nonconvex surrogates involving many parameters. In this study, we proposed a Parameter-Free Non-Convex Tensor Completion model (TC-PFNC) for traffic data recovery, in which a log-based relaxation term was designed to approximate tensor algebraic rank. Moreover, previous studies usually assumed the observations are reliable without any outliers. Therefore, we extended the TC-PFNC to a robust version (RTC-PFNC) by modeling potential traffic data outliers, which can recover the missing value from partial and corrupted observations and remove the anomalies in observations. The numerical solutions of TC-PFNC and RTC-PFNC were elaborated based on the alternating direction multiplier method (ADMM). The extensive experimental results conducted on four real-world traffic data sets demonstrated that the proposed methods outperform other state-of-the-art methods in both missing and corrupted data recovery. The code used in this paper is available at: https://github.com/YoungHe49/T-ITSPFNC.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge