Q-Distribution guided Q-learning for offline reinforcement learning: Uncertainty penalized Q-value via consistency model

``Distribution shift'' is the main obstacle to the success of offline reinforcement learning. A learning policy may take actions beyond the behavior policy's knowledge, referred to as Out-of-Distribution (OOD) actions. The Q-values for these OOD actions can be easily overestimated. As a result, the learning policy is biased by using incorrect Q-value estimates. One common approach to avoid Q-value overestimation is to make a pessimistic adjustment. Our key idea is to penalize the Q-values of OOD actions associated with high uncertainty. In this work, we propose Q-Distribution Guided Q-Learning (QDQ), which applies a pessimistic adjustment to Q-values in OOD regions based on uncertainty estimation. This uncertainty measure relies on the conditional Q-value distribution, learned through a high-fidelity and efficient consistency model. Additionally, to prevent overly conservative estimates, we introduce an uncertainty-aware optimization objective for updating the Q-value function. The proposed QDQ demonstrates solid theoretical guarantees for the accuracy of Q-value distribution learning and uncertainty measurement, as well as the performance of the learning policy. QDQ consistently shows strong performance on the D4RL benchmark and achieves significant improvements across many tasks.

Diffusion Actor-Critic: Formulating Constrained Policy Iteration as Diffusion Noise Regression for Offline Reinforcement Learning

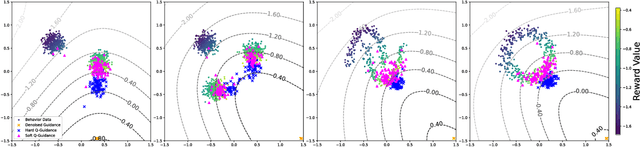
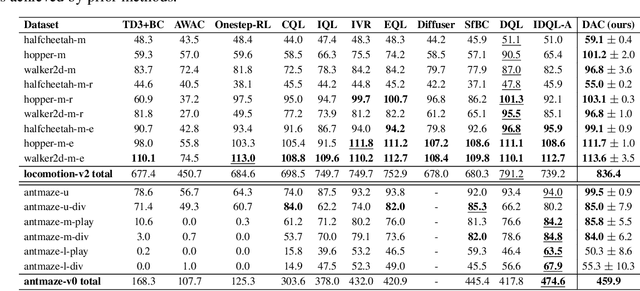
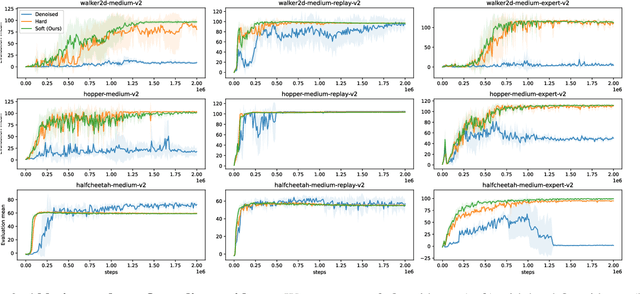
In offline reinforcement learning (RL), it is necessary to manage out-of-distribution actions to prevent overestimation of value functions. Policy-regularized methods address this problem by constraining the target policy to stay close to the behavior policy. Although several approaches suggest representing the behavior policy as an expressive diffusion model to boost performance, it remains unclear how to regularize the target policy given a diffusion-modeled behavior sampler. In this paper, we propose Diffusion Actor-Critic (DAC) that formulates the Kullback-Leibler (KL) constraint policy iteration as a diffusion noise regression problem, enabling direct representation of target policies as diffusion models. Our approach follows the actor-critic learning paradigm that we alternatively train a diffusion-modeled target policy and a critic network. The actor training loss includes a soft Q-guidance term from the Q-gradient. The soft Q-guidance grounds on the theoretical solution of the KL constraint policy iteration, which prevents the learned policy from taking out-of-distribution actions. For critic training, we train a Q-ensemble to stabilize the estimation of Q-gradient. Additionally, DAC employs lower confidence bound (LCB) to address the overestimation and underestimation of value targets due to function approximation error. Our approach is evaluated on the D4RL benchmarks and outperforms the state-of-the-art in almost all environments. Code is available at \href{https://github.com/Fang-Lin93/DAC}{\texttt{github.com/Fang-Lin93/DAC}}.

Enhanced Bayesian Personalized Ranking for Robust Hard Negative Sampling in Recommender Systems

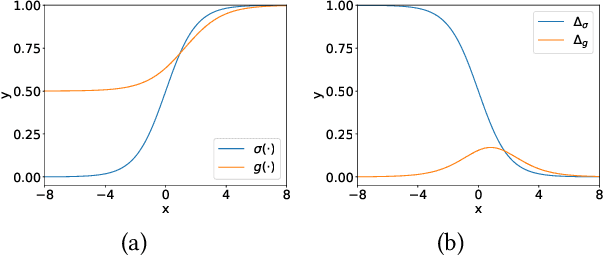
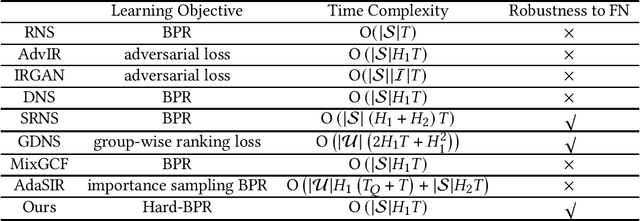
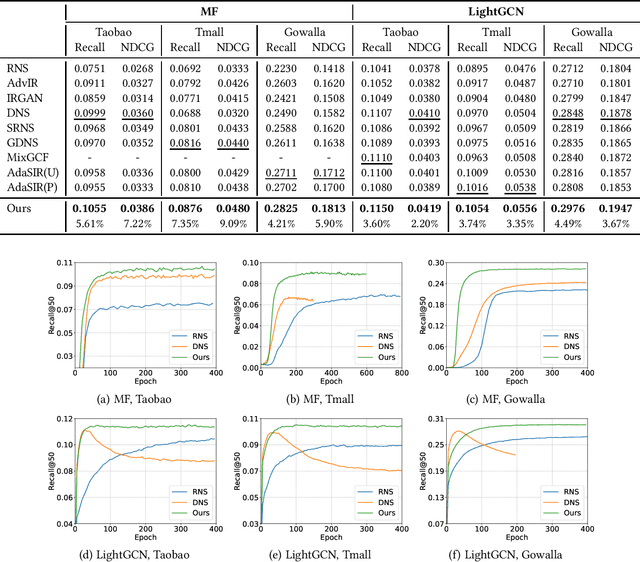
In implicit collaborative filtering, hard negative mining techniques are developed to accelerate and enhance the recommendation model learning. However, the inadvertent selection of false negatives remains a major concern in hard negative sampling, as these false negatives can provide incorrect information and mislead the model learning. To date, only a small number of studies have been committed to solve the false negative problem, primarily focusing on designing sophisticated sampling algorithms to filter false negatives. In contrast, this paper shifts its focus to refining the loss function. We find that the original Bayesian Personalized Ranking (BPR), initially designed for uniform negative sampling, is inadequate in adapting to hard sampling scenarios. Hence, we introduce an enhanced Bayesian Personalized Ranking objective, named as Hard-BPR, which is specifically crafted for dynamic hard negative sampling to mitigate the influence of false negatives. This method is simple yet efficient for real-world deployment. Extensive experiments conducted on three real-world datasets demonstrate the effectiveness and robustness of our approach, along with the enhanced ability to distinguish false negatives.