Distance-weighted Support Vector Machine

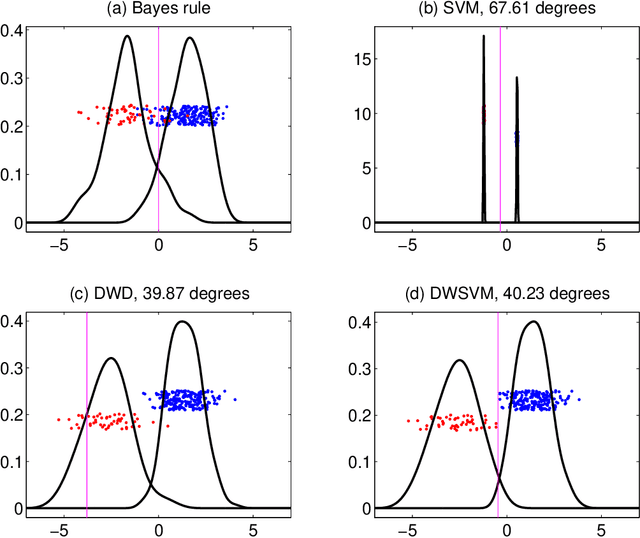
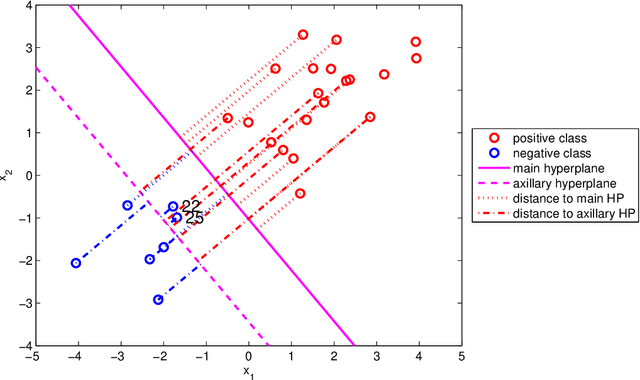
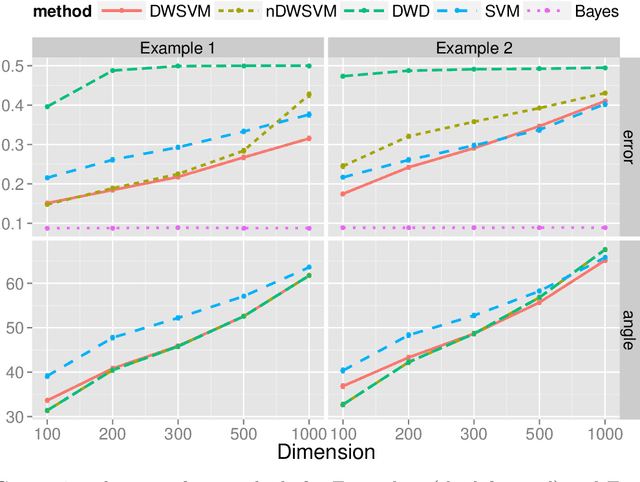
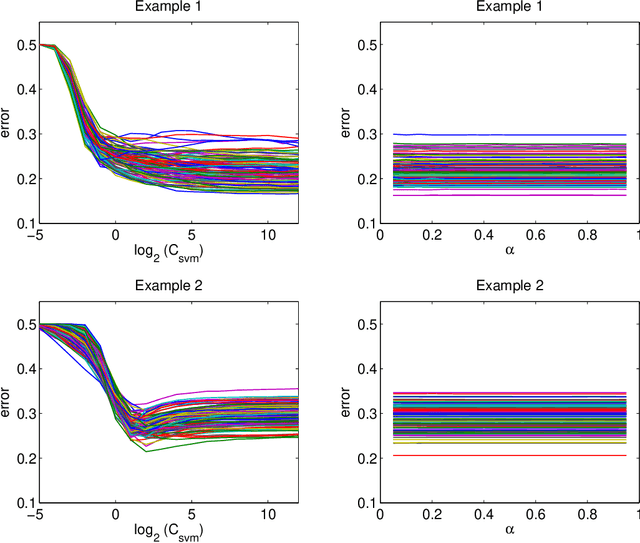
A novel linear classification method that possesses the merits of both the Support Vector Machine (SVM) and the Distance-weighted Discrimination (DWD) is proposed in this article. The proposed Distance-weighted Support Vector Machine method can be viewed as a hybrid of SVM and DWD that finds the classification direction by minimizing mainly the DWD loss, and determines the intercept term in the SVM manner. We show that our method inheres the merit of DWD, and hence, overcomes the data-piling and overfitting issue of SVM. On the other hand, the new method is not subject to imbalanced data issue which was a main advantage of SVM over DWD. It uses an unusual loss which combines the Hinge loss (of SVM) and the DWD loss through a trick of axillary hyperplane. Several theoretical properties, including Fisher consistency and asymptotic normality of the DWSVM solution are developed. We use some simulated examples to show that the new method can compete DWD and SVM on both classification performance and interpretability. A real data application further establishes the usefulness of our approach.

Flexible High-dimensional Classification Machines and Their Asymptotic Properties

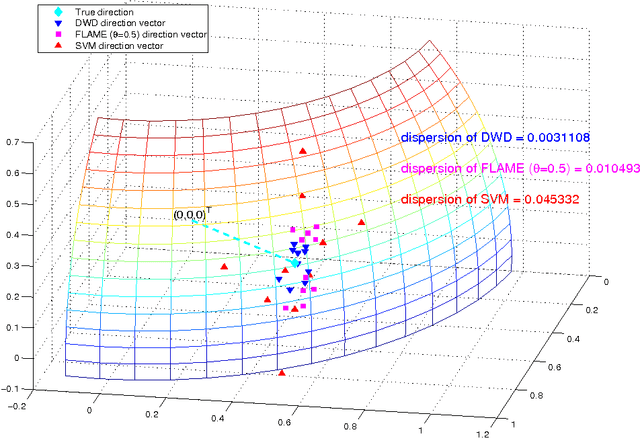
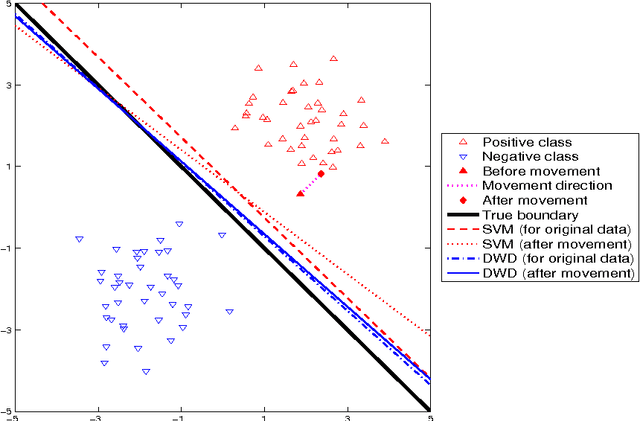
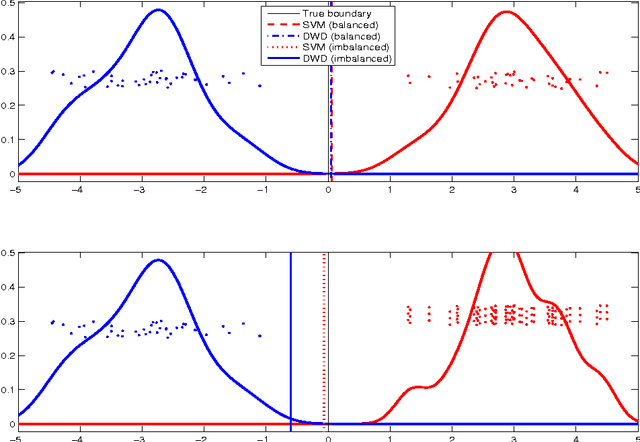
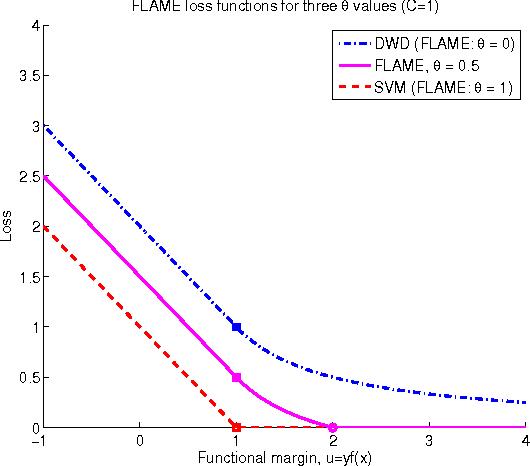
Classification is an important topic in statistics and machine learning with great potential in many real applications. In this paper, we investigate two popular large margin classification methods, Support Vector Machine (SVM) and Distance Weighted Discrimination (DWD), under two contexts: the high-dimensional, low-sample size data and the imbalanced data. A unified family of classification machines, the FLexible Assortment MachinE (FLAME) is proposed, within which DWD and SVM are special cases. The FLAME family helps to identify the similarities and differences between SVM and DWD. It is well known that many classifiers overfit the data in the high-dimensional setting; and others are sensitive to the imbalanced data, that is, the class with a larger sample size overly influences the classifier and pushes the decision boundary towards the minority class. SVM is resistant to the imbalanced data issue, but it overfits high-dimensional data sets by showing the undesired data-piling phenomena. The DWD method was proposed to improve SVM in the high-dimensional setting, but its decision boundary is sensitive to the imbalanced ratio of sample sizes. Our FLAME family helps to understand an intrinsic connection between SVM and DWD, and improves both methods by providing a better trade-off between sensitivity to the imbalanced data and overfitting the high-dimensional data. Several asymptotic properties of the FLAME classifiers are studied. Simulations and real data applications are investigated to illustrate the usefulness of the FLAME classifiers.

Nested Nonnegative Cone Analysis

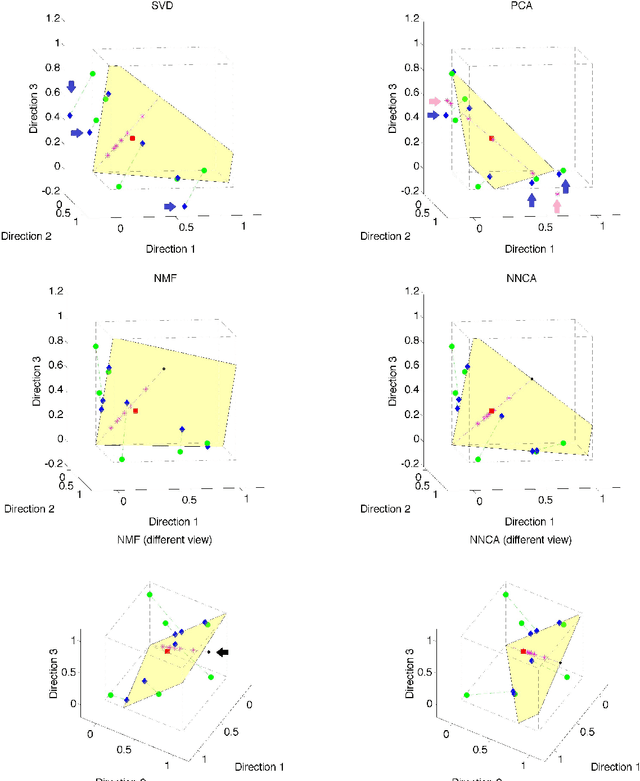
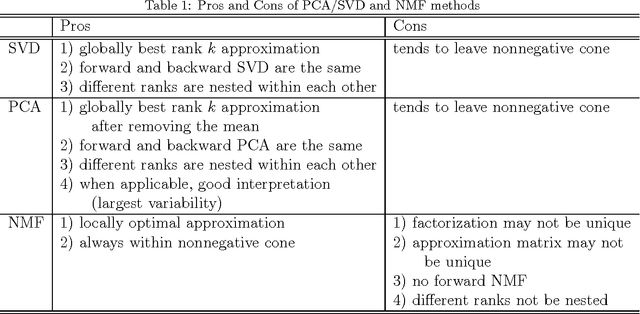
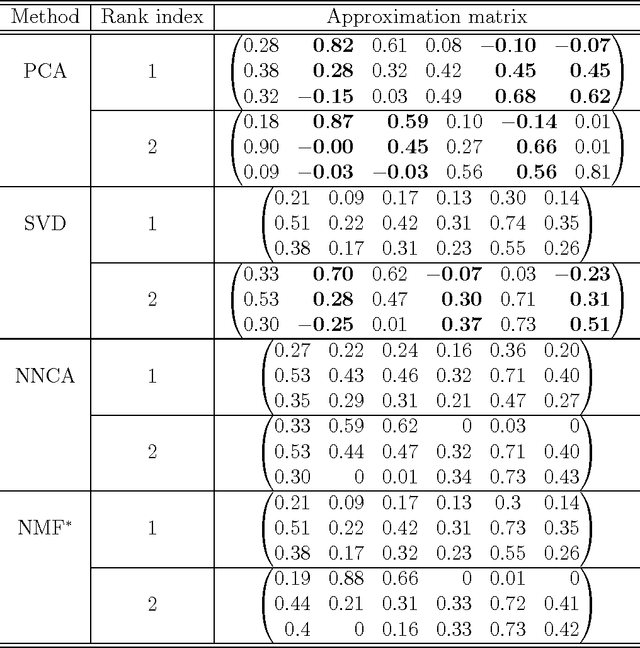
Motivated by the analysis of nonnegative data objects, a novel Nested Nonnegative Cone Analysis (NNCA) approach is proposed to overcome some drawbacks of existing methods. The application of traditional PCA/SVD method to nonnegative data often cause the approximation matrix leave the nonnegative cone, which leads to non-interpretable and sometimes nonsensical results. The nonnegative matrix factorization (NMF) approach overcomes this issue, however the NMF approximation matrices suffer several drawbacks: 1) the factorization may not be unique, 2) the resulting approximation matrix at a specific rank may not be unique, and 3) the subspaces spanned by the approximation matrices at different ranks may not be nested. These drawbacks will cause troubles in determining the number of components and in multi-scale (in ranks) interpretability. The NNCA approach proposed in this paper naturally generates a nested structure, and is shown to be unique at each rank. Simulations are used in this paper to illustrate the drawbacks of the traditional methods, and the usefulness of the NNCA method.

Spatial Multiresolution Cluster Detection Method

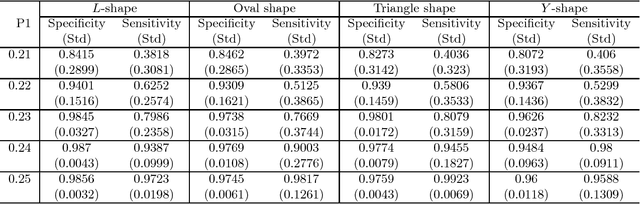
A novel multi-resolution cluster detection (MCD) method is proposed to identify irregularly shaped clusters in space. Multi-scale test statistic on a single cell is derived based on likelihood ratio statistic for Bernoulli sequence, Poisson sequence and Normal sequence. A neighborhood variability measure is defined to select the optimal test threshold. The MCD method is compared with single scale testing methods controlling for false discovery rate and the spatial scan statistics using simulation and f-MRI data. The MCD method is shown to be more effective for discovering irregularly shaped clusters, and the implementation of this method does not require heavy computation, making it suitable for cluster detection for large spatial data.