Detection Is Tracking: Point Cloud Multi-Sweep Deep Learning Models Revisited

Conventional tracking paradigm takes in instantaneous measurements such as range and bearing, and produces object tracks across time. In applications such as autonomous driving, lidar measurements in the form of point clouds are usually passed through a "virtual sensor" realized by a deep learning model, to produce "measurements" such as bounding boxes, which are in turn ingested by a tracking module to produce object tracks. Very often multiple lidar sweeps are accumulated in a buffer to merge and become the input to the virtual sensor. We argue in this paper that such an input already contains temporal information, and therefore the virtual sensor output should also contain temporal information, not just instantaneous values for the time corresponding to the end of the buffer. In particular, we present the deep learning model called MULti-Sweep PAired Detector (MULSPAD) that produces, for each detected object, a pair of bounding boxes at both the end time and the beginning time of the input buffer. This is achieved with fairly straightforward changes in commonly used lidar detection models, and with only marginal extra processing, but the resulting symmetry is satisfying. Such paired detections make it possible not only to construct rudimentary trackers fairly easily, but also to construct more sophisticated trackers that can exploit the extra information conveyed by the pair and be robust to choices of motion models and object birth/death models. We have conducted preliminary training and experimentation using Waymo Open Dataset, which shows the efficacy of our proposed method.

MotionTrack: End-to-End Transformer-based Multi-Object Tracing with LiDAR-Camera Fusion

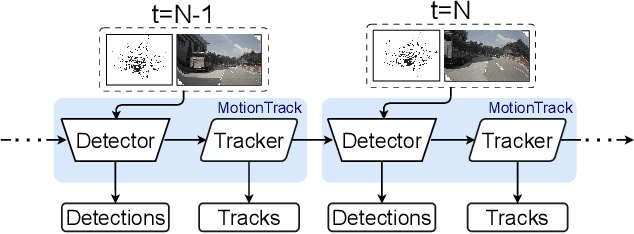
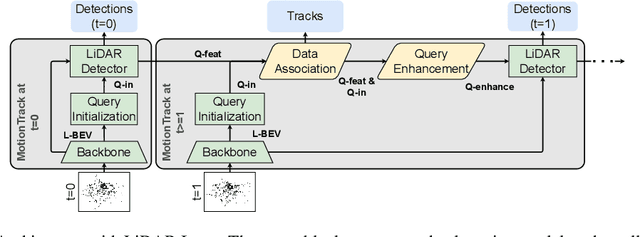
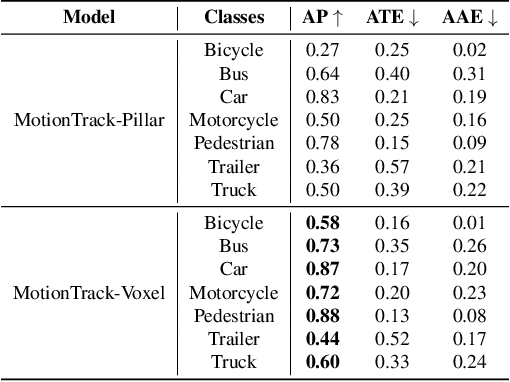
Multiple Object Tracking (MOT) is crucial to autonomous vehicle perception. End-to-end transformer-based algorithms, which detect and track objects simultaneously, show great potential for the MOT task. However, most existing methods focus on image-based tracking with a single object category. In this paper, we propose an end-to-end transformer-based MOT algorithm (MotionTrack) with multi-modality sensor inputs to track objects with multiple classes. Our objective is to establish a transformer baseline for the MOT in an autonomous driving environment. The proposed algorithm consists of a transformer-based data association (DA) module and a transformer-based query enhancement module to achieve MOT and Multiple Object Detection (MOD) simultaneously. The MotionTrack and its variations achieve better results (AMOTA score at 0.55) on the nuScenes dataset compared with other classical baseline models, such as the AB3DMOT, the CenterTrack, and the probabilistic 3D Kalman filter. In addition, we prove that a modified attention mechanism can be utilized for DA to accomplish the MOT, and aggregate history features to enhance the MOD performance.

Multi-Target Tracking with Dependent Likelihood Structures in Labeled Random Finite Set Filters

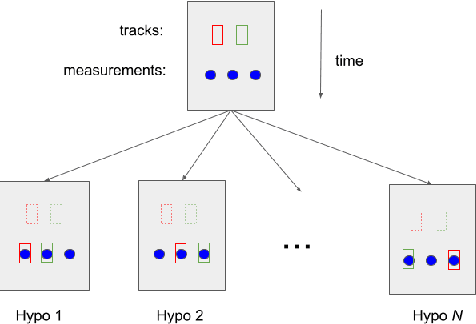
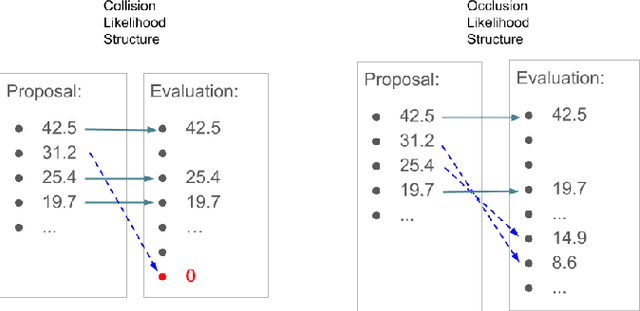
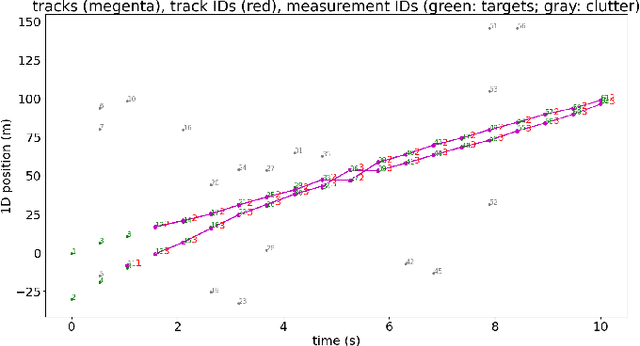
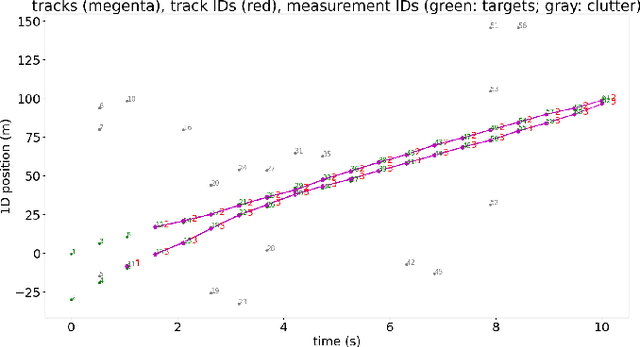
In multi-target tracking, a data association hypothesis assigns measurements to tracks, and the hypothesis likelihood (of the joint target-measurement associations) is used to compare among all hypotheses for truncation under a finite compute budget. It is often assumed however that an individual target-measurement association likelihood is independent of others, i.e., it remains the same in whichever hypothesis it belongs to. In the case of Track Oriented Multiple Hypothesis Tracking (TO-MHT), this leads to a parsimonious representation of the hypothesis space, with a maximum likelihood solution obtained through solving an Integer Linear Programming problem. In Labeled Random Finite Set (Labeled RFS) filters, this leads to an efficient way of obtaining the top ranked hypotheses through solving a ranked assignment problem using Murty's algorithm. In this paper we present a Propose and Verify approach for certain Dependent Likelihood Structures, such that the true hypothesis likelihood is evaluated jointly for the constituent track-measurement associations to account for dependence among them, but at the same time that ranking is still obtained efficiently. This is achieved by proposing a candidate ranking under an assumption of independence, and then evaluating the true likelihood one by one, which is guaranteed, for certain Dependent Likelihood Structures, to not increase from its candidate value, until the desired number of top ranked hypotheses are obtained. Examples of such Dependent Likelihood Structures include the Collision Likelihood Structure and the Occlusion Likelihood Structure, both encountered frequently in applications.