Multi-Target Tracking with Dependent Likelihood Structures in Labeled Random Finite Set Filters

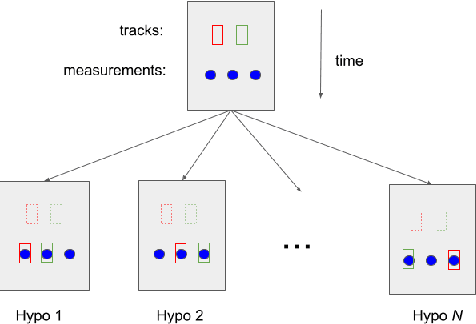
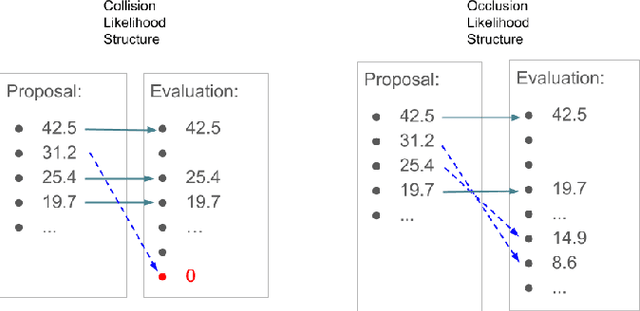
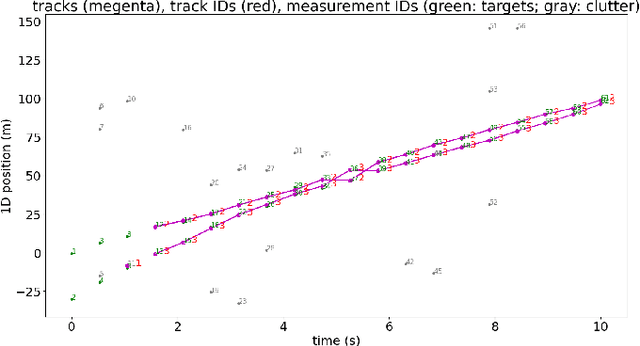
In multi-target tracking, a data association hypothesis assigns measurements to tracks, and the hypothesis likelihood (of the joint target-measurement associations) is used to compare among all hypotheses for truncation under a finite compute budget. It is often assumed however that an individual target-measurement association likelihood is independent of others, i.e., it remains the same in whichever hypothesis it belongs to. In the case of Track Oriented Multiple Hypothesis Tracking (TO-MHT), this leads to a parsimonious representation of the hypothesis space, with a maximum likelihood solution obtained through solving an Integer Linear Programming problem. In Labeled Random Finite Set (Labeled RFS) filters, this leads to an efficient way of obtaining the top ranked hypotheses through solving a ranked assignment problem using Murty's algorithm. In this paper we present a Propose and Verify approach for certain Dependent Likelihood Structures, such that the true hypothesis likelihood is evaluated jointly for the constituent track-measurement associations to account for dependence among them, but at the same time that ranking is still obtained efficiently. This is achieved by proposing a candidate ranking under an assumption of independence, and then evaluating the true likelihood one by one, which is guaranteed, for certain Dependent Likelihood Structures, to not increase from its candidate value, until the desired number of top ranked hypotheses are obtained. Examples of such Dependent Likelihood Structures include the Collision Likelihood Structure and the Occlusion Likelihood Structure, both encountered frequently in applications.