Cross-Domain Label Propagation for Domain Adaptation with Discriminative Graph Self-Learning

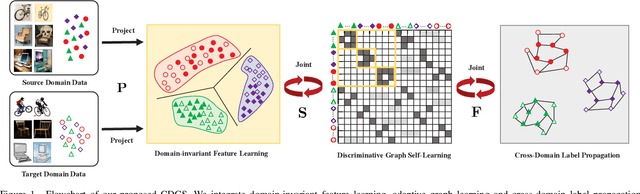
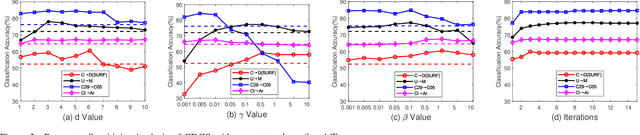
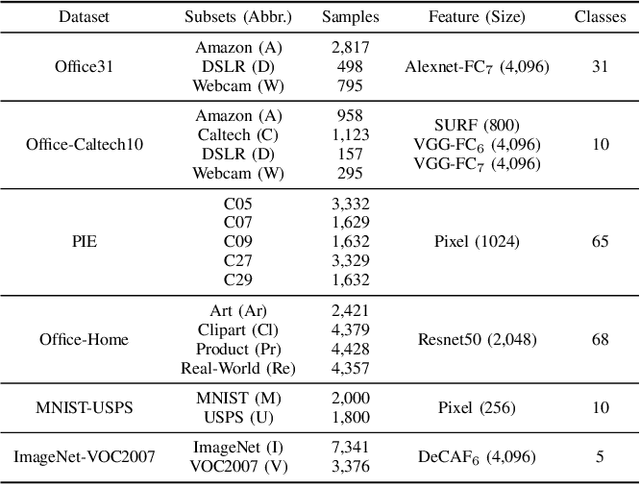
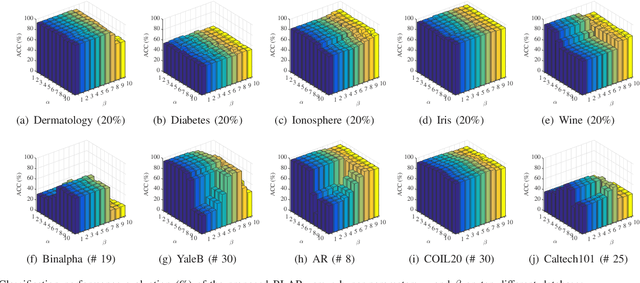
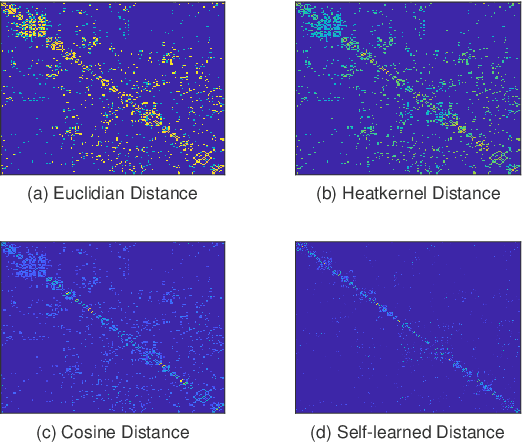
Domain adaptation manages to transfer the knowledge of well-labeled source data to unlabeled target data. Many recent efforts focus on improving the prediction accuracy of target pseudo-labels to reduce conditional distribution shift. In this paper, we propose a novel domain adaptation method, which infers target pseudo-labels through cross-domain label propagation, such that the underlying manifold structure of two domain data can be explored. Unlike existing cross-domain label propagation methods that separate domain-invariant feature learning, affinity matrix constructing and target labels inferring into three independent stages, we propose to integrate them into a unified optimization framework. In such way, these three parts can boost each other from an iterative optimization perspective and thus more effective knowledge transfer can be achieved. Furthermore, to construct a high-quality affinity matrix, we propose a discriminative graph self-learning strategy, which can not only adaptively capture the inherent similarity of the data from two domains but also effectively exploit the discriminative information contained in well-labeled source data and pseudo-labeled target data. An efficient iterative optimization algorithm is designed to solve the objective function of our proposal. Notably, the proposed method can be extended to semi-supervised domain adaptation in a simple but effective way and the corresponding optimization problem can be solved with the identical algorithm. Extensive experiments on six standard datasets verify the significant superiority of our proposal in both unsupervised and semi-supervised domain adaptation settings.

Robust Locality-Aware Regression for Labeled Data Classification

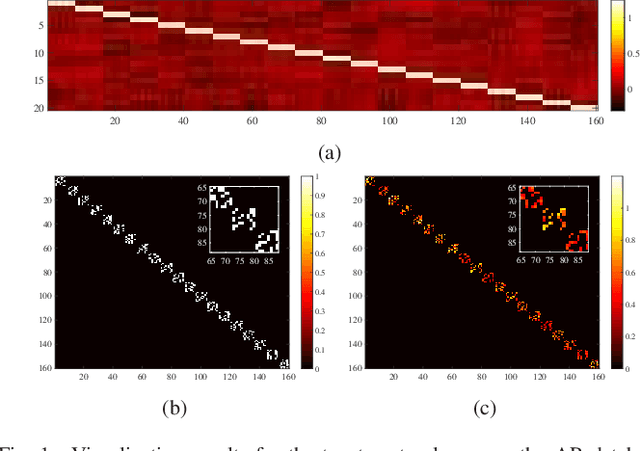
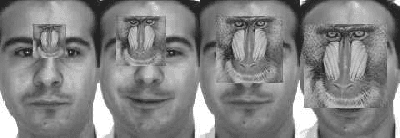
With the dramatic increase of dimensions in the data representation, extracting latent low-dimensional features becomes of the utmost importance for efficient classification. Aiming at the problems of unclear margin representation and difficulty in revealing the data manifold structure in most of the existing linear discriminant methods, we propose a new discriminant feature extraction framework, namely Robust Locality-Aware Regression (RLAR). In our model, we introduce a retargeted regression to perform the marginal representation learning adaptively instead of using the general average inter-class margin. Besides, we formulate a new strategy for enhancing the local intra-class compactness of the data manifold, which can achieve the joint learning of locality-aware graph structure and desirable projection matrix. To alleviate the disturbance of outliers and prevent overfitting, we measure the regression term and locality-aware term together with the regularization term by the L2,1 norm. Further, forcing the row sparsity on the projection matrix through the L2,1 norm achieves the cooperation of feature selection and feature extraction. Then, we derive an effective iterative algorithm for solving the proposed model. The experimental results over a range of UCI data sets and other benchmark databases demonstrate that the proposed RLAR outperforms some state-of-the-art approaches.

Domain Adaptation by Class Centroid Matching and Local Manifold Self-Learning

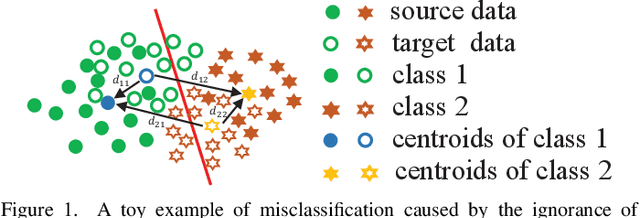
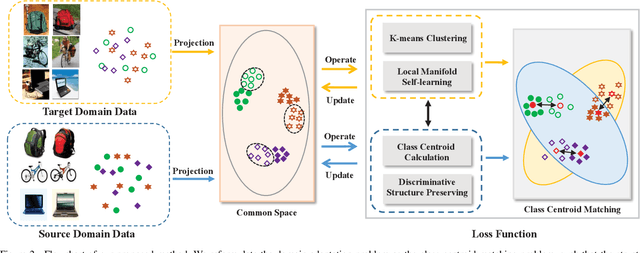
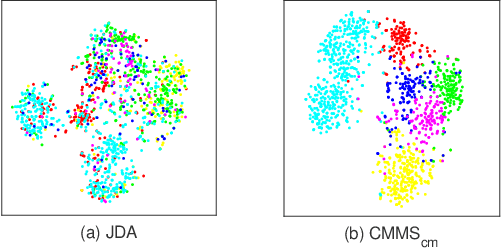
Domain adaptation has been a fundamental technology for transferring knowledge from a source domain to a target domain. The key issue of domain adaptation is how to reduce the distribution discrepancy between two domains in a proper way such that they can be treated indifferently for learning. Different from existing methods that make label prediction for target samples independently, in this paper, we propose a novel domain adaptation approach that assigns pseudo-labels to target data with the guidance of class centroids in two domains, so that the data distribution structure of both source and target domains can be emphasized. Besides, to explore the structure information of target data more thoroughly, we further introduce a local connectivity self-learning strategy into our proposal to adaptively capture the inherent local manifold structure of target samples. The aforementioned class centroid matching and local manifold self-learning are integrated into one joint optimization problem and an iterative optimization algorithm is designed to solve it with theoretical convergence guarantee. In addition to unsupervised domain adaptation, we further extend our method to the semi-supervised scenario including both homogeneous and heterogeneous settings in a direct but elegant way. Extensive experiments on five benchmark datasets validate the significant superiority of our proposal in both unsupervised and semi-supervised manners.