Levente Kocsis
Online Machine Learning in Big Data Streams
Feb 16, 2018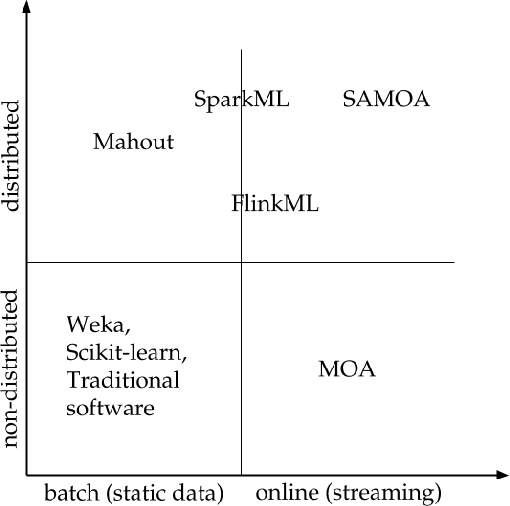

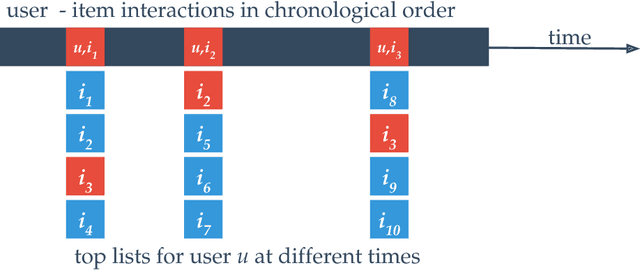
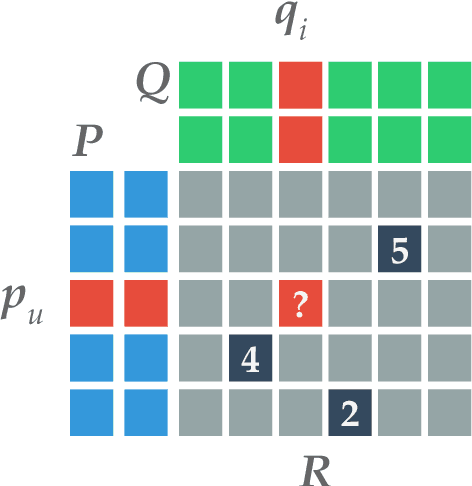
Abstract:The area of online machine learning in big data streams covers algorithms that are (1) distributed and (2) work from data streams with only a limited possibility to store past data. The first requirement mostly concerns software architectures and efficient algorithms. The second one also imposes nontrivial theoretical restrictions on the modeling methods: In the data stream model, older data is no longer available to revise earlier suboptimal modeling decisions as the fresh data arrives. In this article, we provide an overview of distributed software architectures and libraries as well as machine learning models for online learning. We highlight the most important ideas for classification, regression, recommendation, and unsupervised modeling from streaming data, and we show how they are implemented in various distributed data stream processing systems. This article is a reference material and not a survey. We do not attempt to be comprehensive in describing all existing methods and solutions; rather, we give pointers to the most important resources in the field. All related sub-fields, online algorithms, online learning, and distributed data processing are hugely dominant in current research and development with conceptually new research results and software components emerging at the time of writing. In this article, we refer to several survey results, both for distributed data processing and for online machine learning. Compared to past surveys, our article is different because we discuss recommender systems in extended detail.
Efficient Multi-Start Strategies for Local Search Algorithms
Jan 16, 2014



Abstract:Local search algorithms applied to optimization problems often suffer from getting trapped in a local optimum. The common solution for this deficiency is to restart the algorithm when no progress is observed. Alternatively, one can start multiple instances of a local search algorithm, and allocate computational resources (in particular, processing time) to the instances depending on their behavior. Hence, a multi-start strategy has to decide (dynamically) when to allocate additional resources to a particular instance and when to start new instances. In this paper we propose multi-start strategies motivated by works on multi-armed bandit problems and Lipschitz optimization with an unknown constant. The strategies continuously estimate the potential performance of each algorithm instance by supposing a convergence rate of the local search algorithm up to an unknown constant, and in every phase allocate resources to those instances that could converge to the optimum for a particular range of the constant. Asymptotic bounds are given on the performance of the strategies. In particular, we prove that at most a quadratic increase in the number of times the target function is evaluated is needed to achieve the performance of a local search algorithm started from the attraction region of the optimum. Experiments are provided using SPSA (Simultaneous Perturbation Stochastic Approximation) and k-means as local search algorithms, and the results indicate that the proposed strategies work well in practice, and, in all cases studied, need only logarithmically more evaluations of the target function as opposed to the theoretically suggested quadratic increase.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge