GINTRIP: Interpretable Temporal Graph Regression using Information bottleneck and Prototype-based method

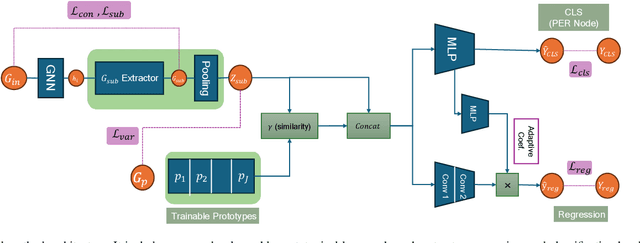
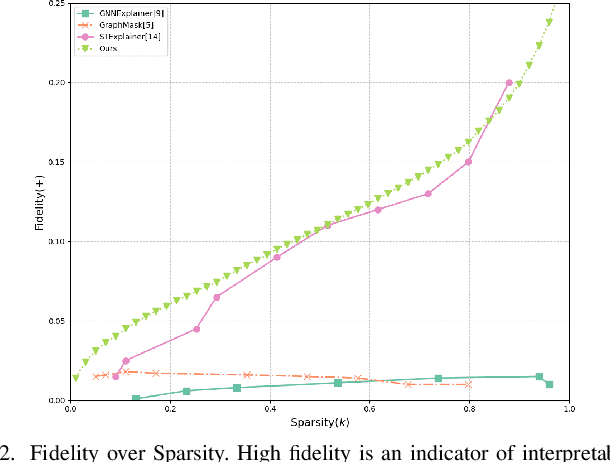
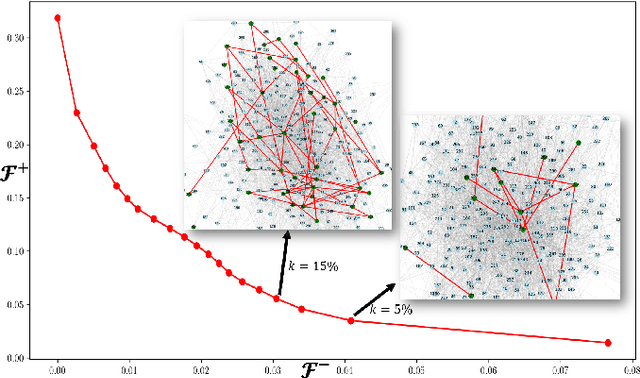
Deep neural networks (DNNs) have demonstrated remarkable performance across various domains, yet their application to temporal graph regression tasks faces significant challenges regarding interpretability. This critical issue, rooted in the inherent complexity of both DNNs and underlying spatio-temporal patterns in the graph, calls for innovative solutions. While interpretability concerns in Graph Neural Networks (GNNs) mirror those of DNNs, to the best of our knowledge, no notable work has addressed the interpretability of temporal GNNs using a combination of Information Bottleneck (IB) principles and prototype-based methods. Our research introduces a novel approach that uniquely integrates these techniques to enhance the interpretability of temporal graph regression models. The key contributions of our work are threefold: We introduce the \underline{G}raph \underline{IN}terpretability in \underline{T}emporal \underline{R}egression task using \underline{I}nformation bottleneck and \underline{P}rototype (GINTRIP) framework, the first combined application of IB and prototype-based methods for interpretable temporal graph tasks. We derive a novel theoretical bound on mutual information (MI), extending the applicability of IB principles to graph regression tasks. We incorporate an unsupervised auxiliary classification head, fostering multi-task learning and diverse concept representation, which enhances the model bottleneck's interpretability. Our model is evaluated on real-world traffic datasets, outperforming existing methods in both forecasting accuracy and interpretability-related metrics.

DIRESA, a distance-preserving nonlinear dimension reduction technique based on regularized autoencoders

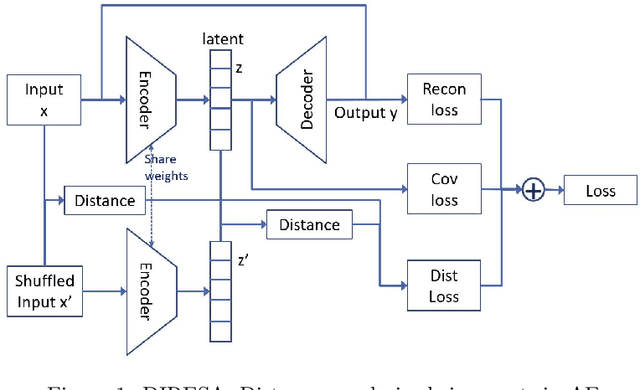
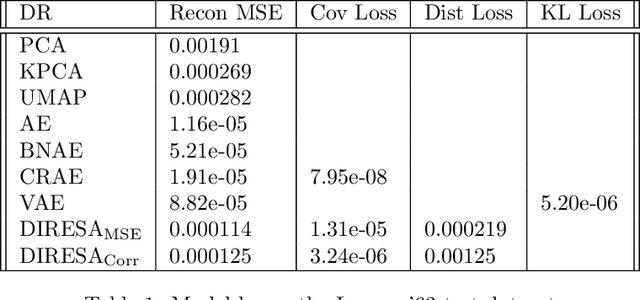
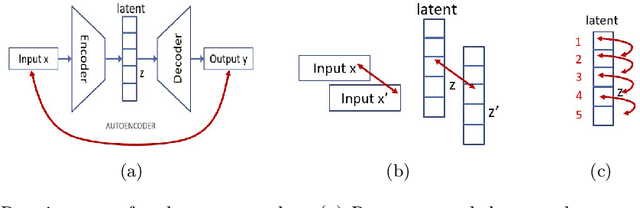
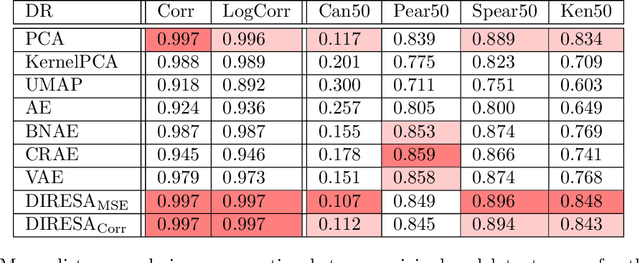
In meteorology, finding similar weather patterns or analogs in historical datasets can be useful for data assimilation, forecasting, and postprocessing. In climate science, analogs in historical and climate projection data are used for attribution and impact studies. However, most of the time, those large weather and climate datasets are nearline. They must be downloaded, which takes a lot of bandwidth and disk space, before the computationally expensive search can be executed. We propose a dimension reduction technique based on autoencoder (AE) neural networks to compress those datasets and perform the search in an interpretable, compressed latent space. A distance-regularized Siamese twin autoencoder (DIRESA) architecture is designed to preserve distance in latent space while capturing the nonlinearities in the datasets. Using conceptual climate models of different complexities, we show that the latent components thus obtained provide physical insight into the dominant modes of variability in the system. Compressing datasets with DIRESA reduces the online storage and keeps the latent components uncorrelated, while the distance (ordering) preservation and reconstruction fidelity robustly outperform Principal Component Analysis (PCA) and other dimension reduction techniques such as UMAP or variational autoencoders.