Combinatorial Continuous Maximal Flows

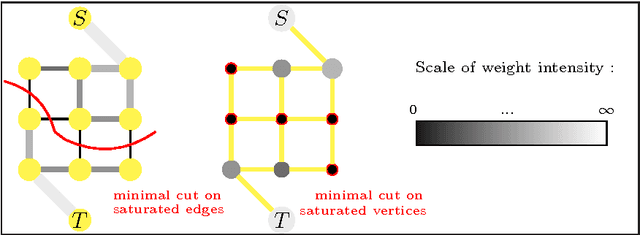
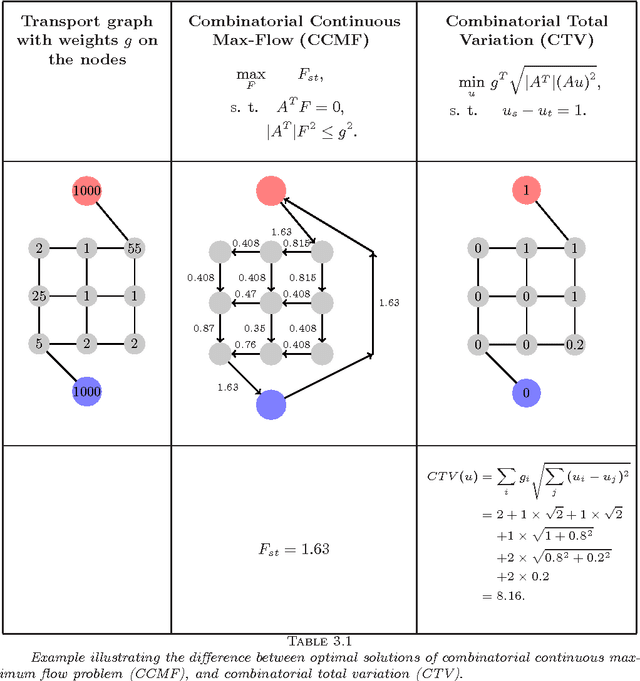
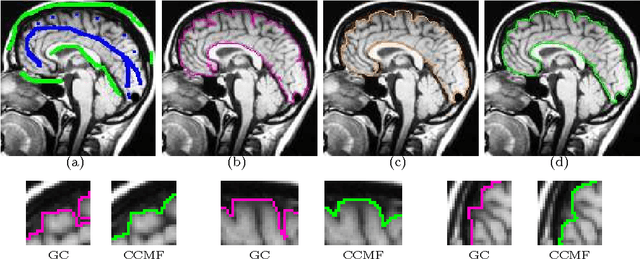
Maximum flow (and minimum cut) algorithms have had a strong impact on computer vision. In particular, graph cuts algorithms provide a mechanism for the discrete optimization of an energy functional which has been used in a variety of applications such as image segmentation, stereo, image stitching and texture synthesis. Algorithms based on the classical formulation of max-flow defined on a graph are known to exhibit metrication artefacts in the solution. Therefore, a recent trend has been to instead employ a spatially continuous maximum flow (or the dual min-cut problem) in these same applications to produce solutions with no metrication errors. However, known fast continuous max-flow algorithms have no stopping criteria or have not been proved to converge. In this work, we revisit the continuous max-flow problem and show that the analogous discrete formulation is different from the classical max-flow problem. We then apply an appropriate combinatorial optimization technique to this combinatorial continuous max-flow CCMF problem to find a null-divergence solution that exhibits no metrication artefacts and may be solved exactly by a fast, efficient algorithm with provable convergence. Finally, by exhibiting the dual problem of our CCMF formulation, we clarify the fact, already proved by Nozawa in the continuous setting, that the max-flow and the total variation problems are not always equivalent.

Optimization of Weighted Curvature for Image Segmentation

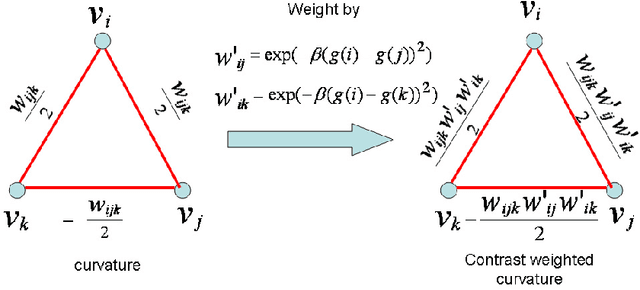
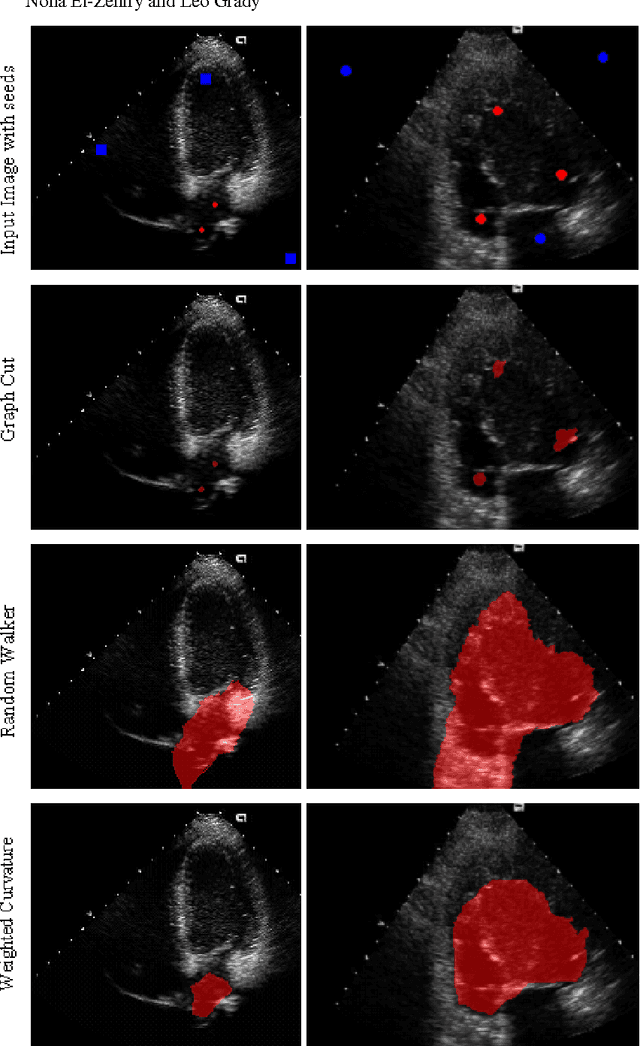
Minimization of boundary curvature is a classic regularization technique for image segmentation in the presence of noisy image data. Techniques for minimizing curvature have historically been derived from descent methods which could be trapped in a local minimum and therefore required a good initialization. Recently, combinatorial optimization techniques have been applied to the optimization of curvature which provide a solution that achieves nearly a global optimum. However, when applied to image segmentation these methods required a meaningful data term. Unfortunately, for many images, particularly medical images, it is difficult to find a meaningful data term. Therefore, we propose to remove the data term completely and instead weight the curvature locally, while still achieving a global optimum.