Optimization of Weighted Curvature for Image Segmentation
Paper and Code
Jun 21, 2010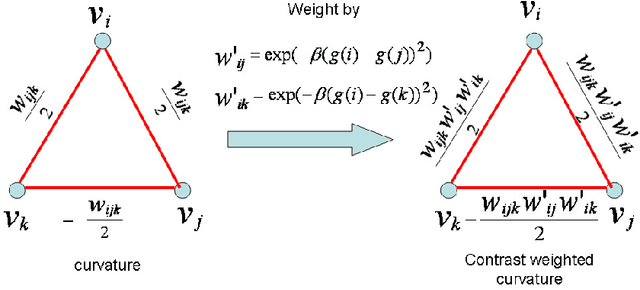


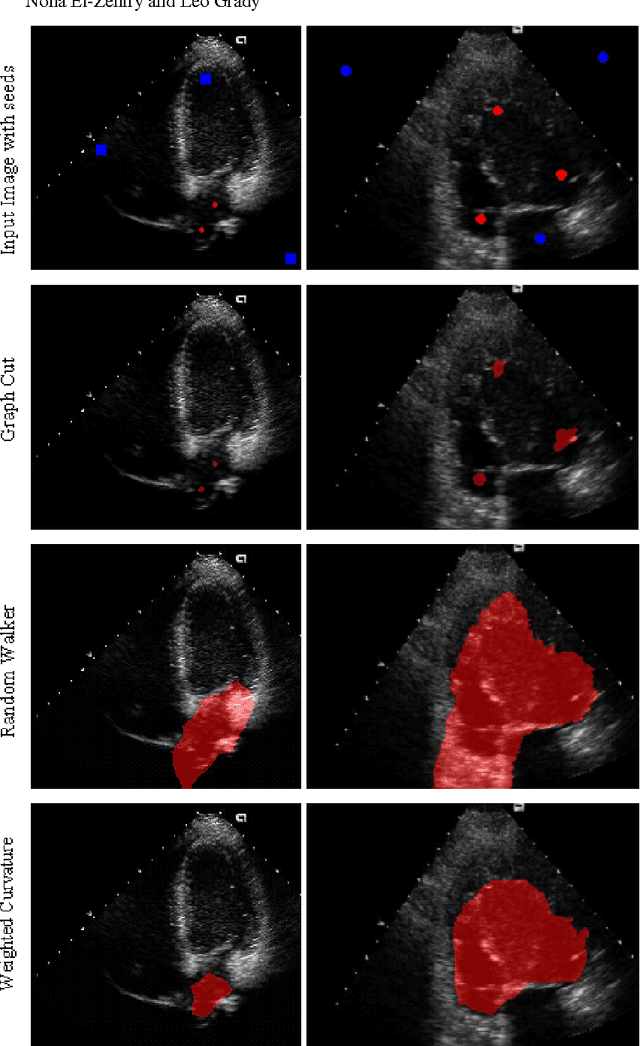
Minimization of boundary curvature is a classic regularization technique for image segmentation in the presence of noisy image data. Techniques for minimizing curvature have historically been derived from descent methods which could be trapped in a local minimum and therefore required a good initialization. Recently, combinatorial optimization techniques have been applied to the optimization of curvature which provide a solution that achieves nearly a global optimum. However, when applied to image segmentation these methods required a meaningful data term. Unfortunately, for many images, particularly medical images, it is difficult to find a meaningful data term. Therefore, we propose to remove the data term completely and instead weight the curvature locally, while still achieving a global optimum.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge