Beyond Trivial Counterfactual Explanations with Diverse Valuable Explanations

Explainability for machine learning models has gained considerable attention within our research community given the importance of deploying more reliable machine-learning systems. In computer vision applications, generative counterfactual methods indicate how to perturb a model's input to change its prediction, providing details about the model's decision-making. Current counterfactual methods make ambiguous interpretations as they combine multiple biases of the model and the data in a single counterfactual interpretation of the model's decision. Moreover, these methods tend to generate trivial counterfactuals about the model's decision, as they often suggest to exaggerate or remove the presence of the attribute being classified. For the machine learning practitioner, these types of counterfactuals offer little value, since they provide no new information about undesired model or data biases. In this work, we propose a counterfactual method that learns a perturbation in a disentangled latent space that is constrained using a diversity-enforcing loss to uncover multiple valuable explanations about the model's prediction. Further, we introduce a mechanism to prevent the model from producing trivial explanations. Experiments on CelebA and Synbols demonstrate that our model improves the success rate of producing high-quality valuable explanations when compared to previous state-of-the-art methods. We will publish the code.

Deep Autoencoders for Dimensionality Reduction of High-Content Screening Data

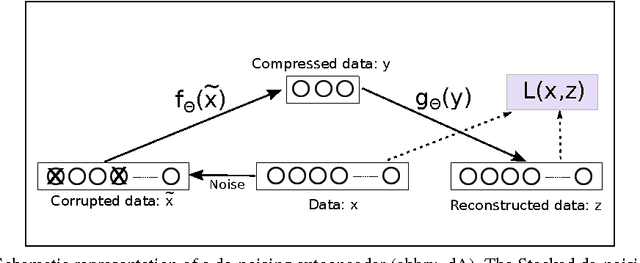
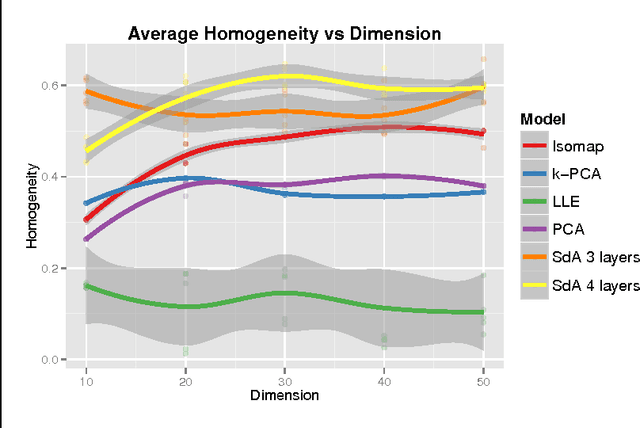
High-content screening uses large collections of unlabeled cell image data to reason about genetics or cell biology. Two important tasks are to identify those cells which bear interesting phenotypes, and to identify sub-populations enriched for these phenotypes. This exploratory data analysis usually involves dimensionality reduction followed by clustering, in the hope that clusters represent a phenotype. We propose the use of stacked de-noising auto-encoders to perform dimensionality reduction for high-content screening. We demonstrate the superior performance of our approach over PCA, Local Linear Embedding, Kernel PCA and Isomap.