Reachset-Conformant System Identification

Formal verification techniques play a pivotal role in ensuring the safety of complex cyber-physical systems. To transfer model-based verification results to the real world, we require that the measurements of the target system lie in the set of reachable outputs of the corresponding model, a property we refer to as reachset conformance. This paper is on automatically identifying those reachset-conformant models. While state-of-the-art reachset-conformant identification methods focus on linear state-space models, we generalize these methods to nonlinear state-space models and linear and nonlinear input-output models. Furthermore, our identification framework adapts to different levels of prior knowledge on the system dynamics. In particular, we identify the set of model uncertainties for white-box models, the parameters and the set of model uncertainties for gray-box models, and entire reachset-conformant black-box models from data. For the black-box identification, we propose a new genetic programming variant, which we call conformant genetic programming. The robustness and efficacy of our framework are demonstrated in extensive numerical experiments using simulated and real-world data.

Reachability Analysis of ARMAX Models

Reachability analysis is a powerful tool for computing the set of states or outputs reachable for a system. While previous work has focused on systems described by state-space models, we present the first methods to compute reachable sets of ARMAX models - one of the most common input-output models originating from data-driven system identification. The first approach we propose can only be used with dependency-preserving set representations such as symbolic zonotopes, while the second one is valid for arbitrary set representations but relies on a reformulation of the ARMAX model. By analyzing the computational complexities, we show that both approaches scale quadratically with respect to the time horizon of the reachability problem when using symbolic zonotopes. To reduce the computational complexity, we propose a third approach that scales linearly with respect to the time horizon when using set representations that are closed under Minkowski addition and linear transformation and that satisfy that the computational complexity of the Minkowski sum is independent of the representation size of the operands. Our numerical experiments demonstrate that the reachable sets of ARMAX models are tighter than the reachable sets of equivalent state space models in case of unknown initial states. Therefore, this methodology has the potential to significantly reduce the conservatism of various verification techniques.

Density Planner: Minimizing Collision Risk in Motion Planning with Dynamic Obstacles using Density-based Reachability

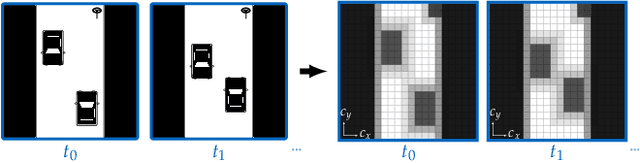
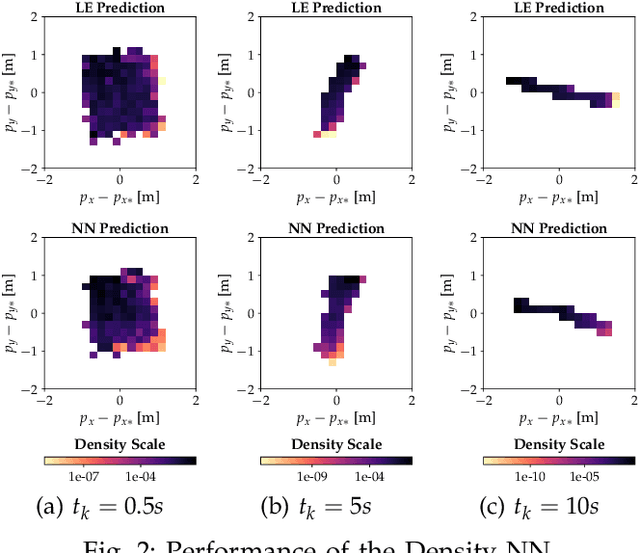
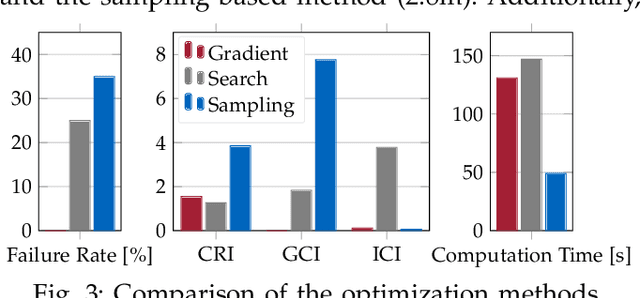
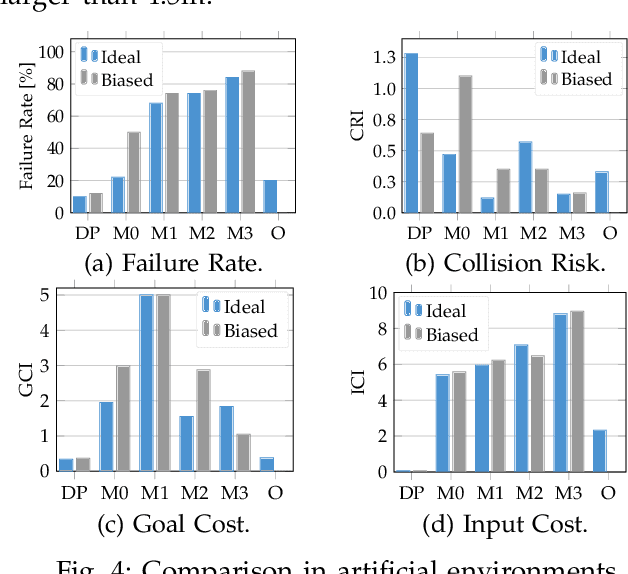
Autonomous systems with uncertainties are prevalent in robotics. However, ensuring the safety of those systems is challenging due to sophisticated dynamics and the hardness to predict future states. Usually, a classical motion planning method considering all possible states will not find a feasible path in crowded environments. To overcome this conservativeness, we propose a density-based method. The proposed method uses a neural network and the Liouville equation to learn the density evolution, and by applying a gradient-based optimization procedure, we can plan for feasible and probably safe trajectories to minimize the collision risk. We conduct experiments on simulated environments and environments generated from real-world data and outperform baseline methods such as model predictive control (MPC) and nonlinear programming (NLP). While our method requires planning time in advance, the online computational complexity is very low when compared to other methods.