Lars Horchens
Deep Learning for Multi-View Ultrasonic Image Fusion
Sep 08, 2021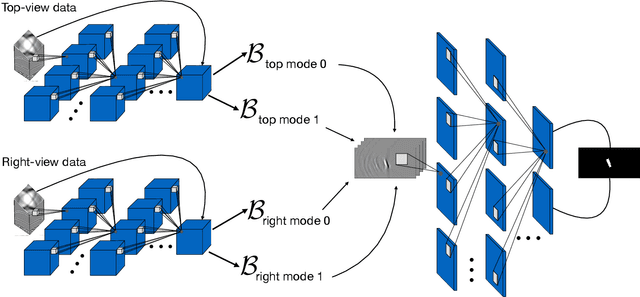
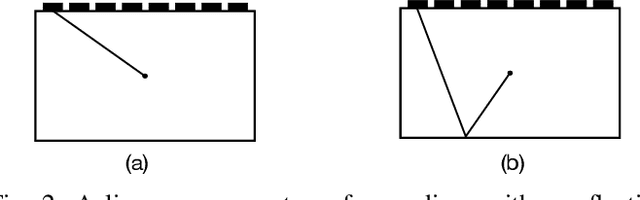
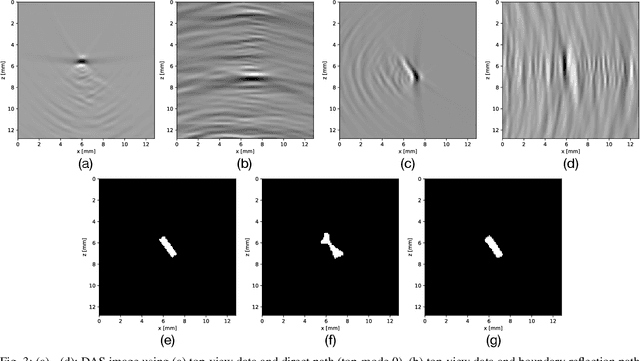
Abstract:Ultrasonic imaging is being used to obtain information about the acoustic properties of a medium by emitting waves into it and recording their interaction using ultrasonic transducer arrays. The Delay-And-Sum (DAS) algorithm forms images using the main path on which reflected signals travel back to the transducers. In some applications, different insonification paths can be considered, for instance by placing the transducers at different locations or if strong reflectors inside the medium are known a-priori. These different modes give rise to multiple DAS images reflecting different geometric information about the scatterers and the challenge is to either fuse them into one image or to directly extract higher-level information regarding the materials of the medium, e.g., a segmentation map. Traditional image fusion techniques typically use ad-hoc combinations of pre-defined image transforms, pooling operations and thresholding. In this work, we propose a deep neural network (DNN) architecture that directly maps all available data to a segmentation map while explicitly incorporating the DAS image formation for the different insonification paths as network layers. This enables information flow between data pre-processing and image post-processing DNNs, trained end-to-end. We compare our proposed method to a traditional image fusion technique using simulated data experiments, mimicking a non-destructive testing application with four image modes, i.e., two transducer locations and two internal reflection boundaries. Using our approach, it is possible to obtain much more accurate segmentation of defects.
Deep data compression for approximate ultrasonic image formation
Sep 04, 2020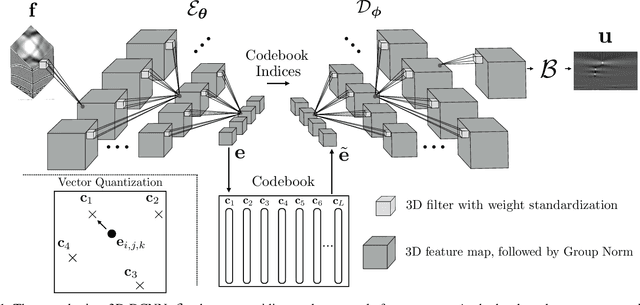
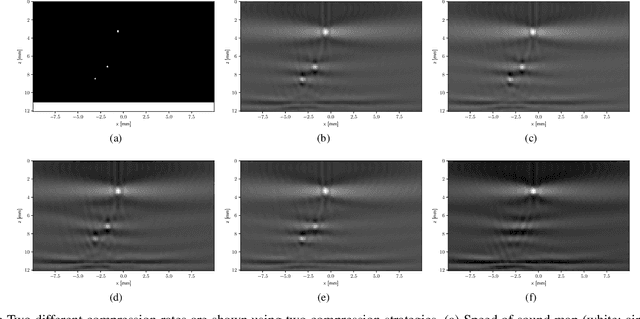
Abstract:In many ultrasonic imaging systems, data acquisition and image formation are performed on separate computing devices. Data transmission is becoming a bottleneck, thus, efficient data compression is essential. Compression rates can be improved by considering the fact that many image formation methods rely on approximations of wave-matter interactions, and only use the corresponding part of the data. Tailored data compression could exploit this, but extracting the useful part of the data efficiently is not always trivial. In this work, we tackle this problem using deep neural networks, optimized to preserve the image quality of a particular image formation method. The Delay-And-Sum (DAS) algorithm is examined which is used in reflectivity-based ultrasonic imaging. We propose a novel encoder-decoder architecture with vector quantization and formulate image formation as a network layer for end-to-end training. Experiments demonstrate that our proposed data compression tailored for a specific image formation method obtains significantly better results as opposed to compression agnostic to subsequent imaging. We maintain high image quality at much higher compression rates than the theoretical lossless compression rate derived from the rank of the linear imaging operator. This demonstrates the great potential of deep ultrasonic data compression tailored for a specific image formation method.
Fast ultrasonic imaging using end-to-end deep learning
Sep 04, 2020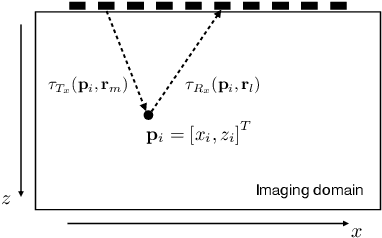
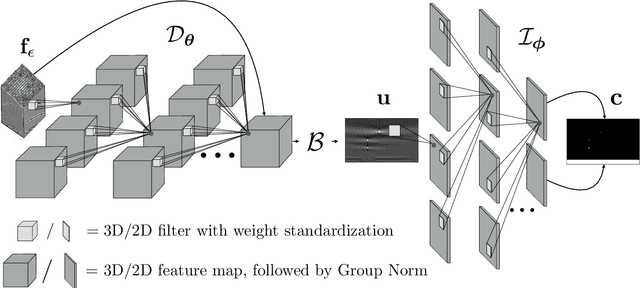
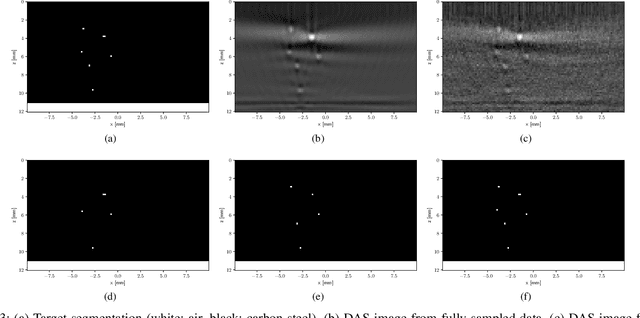
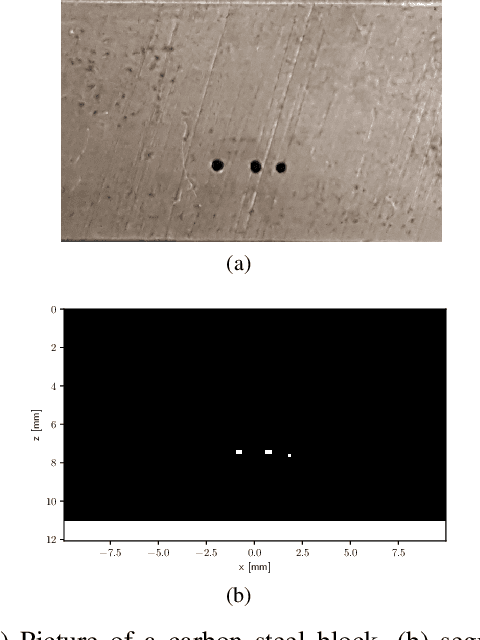
Abstract:Ultrasonic imaging algorithms used in many clinical and industrial applications consist of three steps: A data pre-processing, an image formation and an image post-processing step. For efficiency, image formation often relies on an approximation of the underlying wave physics. A prominent example is the Delay-And-Sum (DAS) algorithm used in reflectivity-based ultrasonic imaging. Recently, deep neural networks (DNNs) are being used for the data pre-processing and the image post-processing steps separately. In this work, we propose a novel deep learning architecture that integrates all three steps to enable end-to-end training. We examine turning the DAS image formation method into a network layer that connects data pre-processing layers with image post-processing layers that perform segmentation. We demonstrate that this integrated approach clearly outperforms sequential approaches that are trained separately. While network training and evaluation is performed only on simulated data, we also showcase the potential of our approach on real data from a non-destructive testing scenario.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge