Training Transformers with Enforced Lipschitz Constants

Neural networks are often highly sensitive to input and weight perturbations. This sensitivity has been linked to pathologies such as vulnerability to adversarial examples, divergent training, and overfitting. To combat these problems, past research has looked at building neural networks entirely from Lipschitz components. However, these techniques have not matured to the point where researchers have trained a modern architecture such as a transformer with a Lipschitz certificate enforced beyond initialization. To explore this gap, we begin by developing and benchmarking novel, computationally-efficient tools for maintaining norm-constrained weight matrices. Applying these tools, we are able to train transformer models with Lipschitz bounds enforced throughout training. We find that optimizer dynamics matter: switching from AdamW to Muon improves standard methods -- weight decay and spectral normalization -- allowing models to reach equal performance with a lower Lipschitz bound. Inspired by Muon's update having a fixed spectral norm, we co-design a weight constraint method that improves the Lipschitz vs. performance tradeoff on MLPs and 2M parameter transformers. Our 2-Lipschitz transformer on Shakespeare text reaches validation accuracy 60%. Scaling to 145M parameters, our 10-Lipschitz transformer reaches 21% accuracy on internet text. However, to match the NanoGPT baseline validation accuracy of 39.4%, our Lipschitz upper bound increases to 10^264. Nonetheless, our Lipschitz transformers train without stability measures such as layer norm, QK norm, and logit tanh softcapping.

Modular Duality in Deep Learning

An old idea in optimization theory says that since the gradient is a dual vector it may not be subtracted from the weights without first being mapped to the primal space where the weights reside. We take this idea seriously in this paper and construct such a duality map for general neural networks. Our map, which we call modular dualization, forms a unifying theoretical basis for training algorithms that are a) fast and b) scalable. Modular dualization involves first assigning operator norms to layers based on the semantics of each layer, and then using these layerwise norms to recursively induce a duality map on the weight space of the full neural architecture. We conclude by deriving GPU-friendly algorithms for dualizing Embed, Linear and Conv2D layers -- the latter two methods are based on a new rectangular Newton-Schulz iteration that we propose. Our iteration was recently used to set new speed records for training NanoGPT. Overall, we hope that our theory of modular duality will yield a next generation of fast and scalable optimizers for general neural architectures.

Old Optimizer, New Norm: An Anthology

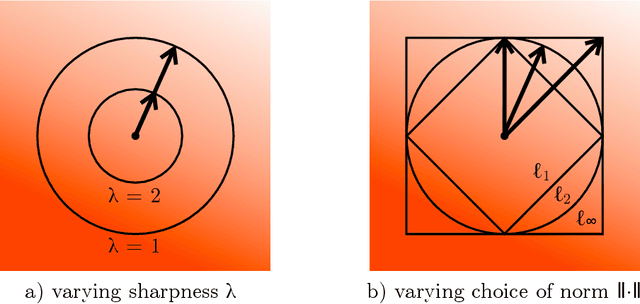
Deep learning optimizers are often motivated through a mix of convex and approximate second-order theory. We select three such methods -- Adam, Shampoo and Prodigy -- and argue that each method can instead be understood as a squarely first-order method without convexity assumptions. In fact, after switching off exponential moving averages, each method is equivalent to steepest descent under a particular norm. By generalizing this observation, we chart a new design space for training algorithms. Different operator norms should be assigned to different tensors based on the role that the tensor plays within the network. For example, while linear and embedding layers may have the same weight space of $\mathbb{R}^{m\times n}$, these layers play different roles and should be assigned different norms. We hope that this idea of carefully metrizing the neural architecture might lead to more stable, scalable and indeed faster training.

Autoregressive Neural TensorNet: Bridging Neural Networks and Tensor Networks for Quantum Many-Body Simulation

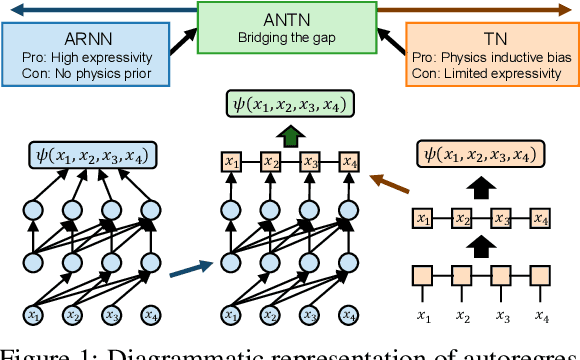
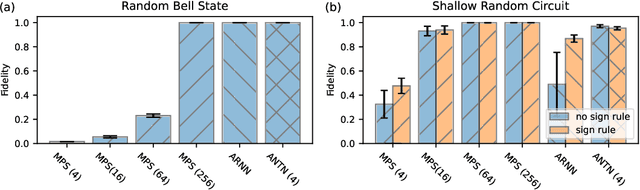
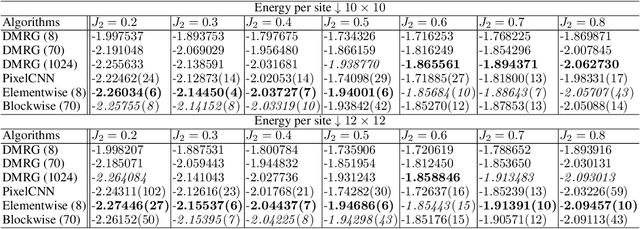
Quantum many-body physics simulation has important impacts on understanding fundamental science and has applications to quantum materials design and quantum technology. However, due to the exponentially growing size of the Hilbert space with respect to the particle number, a direct simulation is intractable. While representing quantum states with tensor networks and neural networks are the two state-of-the-art methods for approximate simulations, each has its own limitations in terms of expressivity and optimization. To address these challenges, we develop a novel architecture, Autoregressive Neural TensorNet (ANTN), which bridges tensor networks and autoregressive neural networks. We show that Autoregressive Neural TensorNet parameterizes normalized wavefunctions with exact sampling, generalizes the expressivity of tensor networks and autoregressive neural networks, and inherits a variety of symmetries from autoregressive neural networks. We demonstrate our approach on the 2D $J_1$-$J_2$ Heisenberg model with different systems sizes and coupling parameters, outperforming both tensor networks and autoregressive neural networks. Our work opens up new opportunities for both scientific simulations and machine learning applications.