Highly Efficient and Unsupervised Framework for Moving Object Detection in Satellite Videos

Moving object detection in satellite videos (SVMOD) is a challenging task due to the extremely dim and small target characteristics. Current learning-based methods extract spatio-temporal information from multi-frame dense representation with labor-intensive manual labels to tackle SVMOD, which needs high annotation costs and contains tremendous computational redundancy due to the severe imbalance between foreground and background regions. In this paper, we propose a highly efficient unsupervised framework for SVMOD. Specifically, we propose a generic unsupervised framework for SVMOD, in which pseudo labels generated by a traditional method can evolve with the training process to promote detection performance. Furthermore, we propose a highly efficient and effective sparse convolutional anchor-free detection network by sampling the dense multi-frame image form into a sparse spatio-temporal point cloud representation and skipping the redundant computation on background regions. Coping these two designs, we can achieve both high efficiency (label and computation efficiency) and effectiveness. Extensive experiments demonstrate that our method can not only process 98.8 frames per second on 1024x1024 images but also achieve state-of-the-art performance. The relabeled dataset and code are available at https://github.com/ChaoXiao12/Moving-object-detection-in-satellite-videos-HiEUM.

On the Number of Linear Regions of Convolutional Neural Networks

One fundamental problem in deep learning is understanding the outstanding performance of deep Neural Networks (NNs) in practice. One explanation for the superiority of NNs is that they can realize a large class of complicated functions, i.e., they have powerful expressivity. The expressivity of a ReLU NN can be quantified by the maximal number of linear regions it can separate its input space into. In this paper, we provide several mathematical results needed for studying the linear regions of CNNs, and use them to derive the maximal and average numbers of linear regions for one-layer ReLU CNNs. Furthermore, we obtain upper and lower bounds for the number of linear regions of multi-layer ReLU CNNs. Our results suggest that deeper CNNs have more powerful expressivity than their shallow counterparts, while CNNs have more expressivity than fully-connected NNs per parameter.

Semantic Segmentation from Limited Training Data

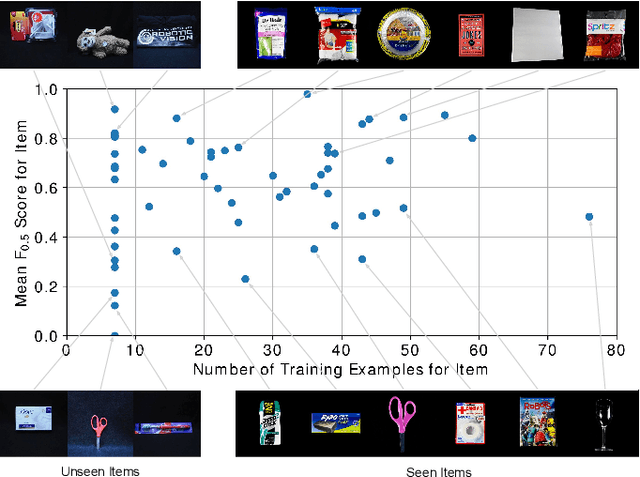
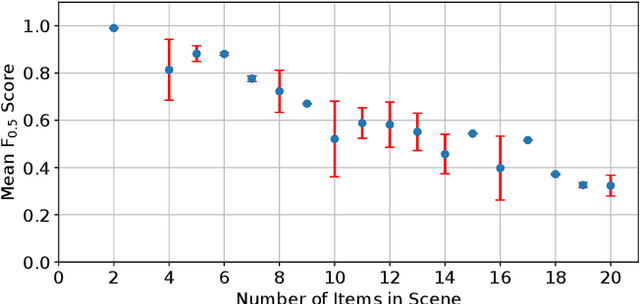
We present our approach for robotic perception in cluttered scenes that led to winning the recent Amazon Robotics Challenge (ARC) 2017. Next to small objects with shiny and transparent surfaces, the biggest challenge of the 2017 competition was the introduction of unseen categories. In contrast to traditional approaches which require large collections of annotated data and many hours of training, the task here was to obtain a robust perception pipeline with only few minutes of data acquisition and training time. To that end, we present two strategies that we explored. One is a deep metric learning approach that works in three separate steps: semantic-agnostic boundary detection, patch classification and pixel-wise voting. The other is a fully-supervised semantic segmentation approach with efficient dataset collection. We conduct an extensive analysis of the two methods on our ARC 2017 dataset. Interestingly, only few examples of each class are sufficient to fine-tune even very deep convolutional neural networks for this specific task.

Minimum Error Tree Decomposition

This paper describes a generalization of previous methods for constructing tree-structured belief network with hidden variables. The major new feature of the described method is the ability to produce a tree decomposition even when there are errors in the correlation data among the input variables. This is an important extension of existing methods since the correlational coefficients usually cannot be measured with precision. The technique involves using a greedy search algorithm that locally minimizes an error function.

Properties and Applications of Programs with Monotone and Convex Constraints

We study properties of programs with monotone and convex constraints. We extend to these formalisms concepts and results from normal logic programming. They include the notions of strong and uniform equivalence with their characterizations, tight programs and Fages Lemma, program completion and loop formulas. Our results provide an abstract account of properties of some recent extensions of logic programming with aggregates, especially the formalism of lparse programs. They imply a method to compute stable models of lparse programs by means of off-the-shelf solvers of pseudo-boolean constraints, which is often much faster than the smodels system.