DiffRed: Dimensionality Reduction guided by stable rank

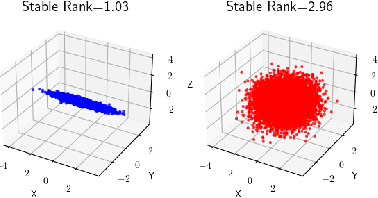
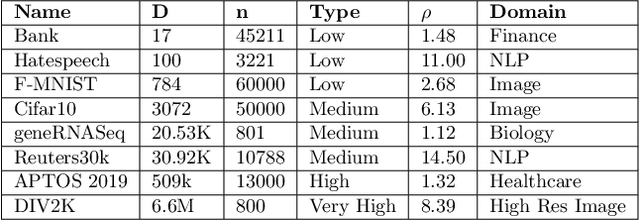
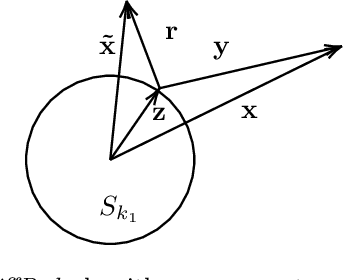
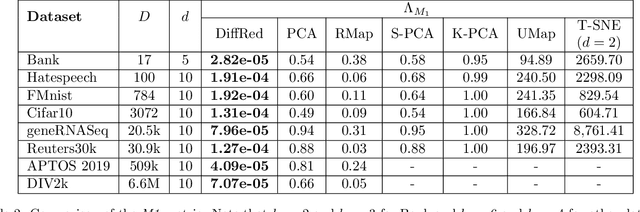
In this work, we propose a novel dimensionality reduction technique, DiffRed, which first projects the data matrix, A, along first $k_1$ principal components and the residual matrix $A^{*}$ (left after subtracting its $k_1$-rank approximation) along $k_2$ Gaussian random vectors. We evaluate M1, the distortion of mean-squared pair-wise distance, and Stress, the normalized value of RMS of distortion of the pairwise distances. We rigorously prove that DiffRed achieves a general upper bound of $O\left(\sqrt{\frac{1-p}{k_2}}\right)$ on Stress and $O\left(\frac{(1-p)}{\sqrt{k_2*\rho(A^{*})}}\right)$ on M1 where $p$ is the fraction of variance explained by the first $k_1$ principal components and $\rho(A^{*})$ is the stable rank of $A^{*}$. These bounds are tighter than the currently known results for Random maps. Our extensive experiments on a variety of real-world datasets demonstrate that DiffRed achieves near zero M1 and much lower values of Stress as compared to the well-known dimensionality reduction techniques. In particular, DiffRed can map a 6 million dimensional dataset to 10 dimensions with 54% lower Stress than PCA.

Uniform Brackets, Containers, and Combinatorial Macbeath Regions

We study the connections between three seemingly different combinatorial structures - "uniform" brackets in statistics and probability theory, "containers" in online and distributed learning theory, and "combinatorial Macbeath regions", or Mnets in discrete and computational geometry. We show that these three concepts are manifestations of a single combinatorial property that can be expressed under a unified framework along the lines of Vapnik-Chervonenkis type theory for uniform convergence. These new connections help us to bring tools from discrete and computational geometry to prove improved bounds for these objects. Our improved bounds help to get an optimal algorithm for distributed learning of halfspaces, an improved algorithm for the distributed convex set disjointness problem, and improved regret bounds for online algorithms against a smoothed adversary for a large class of semi-algebraic threshold functions.

Size sensitive packing number for Hamming cube and its consequences

We prove a size-sensitive version of Haussler's Packing lemma~\cite{Haussler92spherepacking} for set-systems with bounded primal shatter dimension, which have an additional {\em size-sensitive property}. This answers a question asked by Ezra~\cite{Ezra-sizesendisc-soda-14}. We also partially address another point raised by Ezra regarding overcounting of sets in her chaining procedure. As a consequence of these improvements, we get an improvement on the size-sensitive discrepancy bounds for set systems with the above property. Improved bounds on the discrepancy for these special set systems also imply an improvement in the sizes of {\em relative $(\varepsilon, \delta)$-approximations} and $(\nu, \alpha)$-samples.