A Modularized Framework for Piecewise-Stationary Restless Bandits

We study the piecewise-stationary restless multi-armed bandit (PS-RMAB) problem, where each arm evolves as a Markov chain but \emph{mean rewards may change across unknown segments}. To address the resulting exploration--detection delay trade-off, we propose a modular framework that integrates arbitrary RMAB base algorithms with change detection and a novel diminishing exploration mechanism. This design enables flexible plug-and-play use of existing solvers and detectors, while efficiently adapting to mean changes without prior knowledge of their number. To evaluate performance, we introduce a refined regret notion that measures the \emph{excess regret due to exploration and detection}, benchmarked against an oracle that restarts the base algorithm at the true change points. Under this metric, we prove a regret bound of $\tilde{O}(\sqrt{LMKT})$, where $L$ denotes the maximum mixing time of the Markov chains across all arms and segments, $M$ the number of segments, $K$ the number of arms, and $T$ the horizon. Simulations confirm that our framework achieves regret close to that of the segment oracle and consistently outperforms base solvers that do not incorporate any mechanism to handle environmental changes.

Diminishing Exploration: A Minimalist Approach to Piecewise Stationary Multi-Armed Bandits

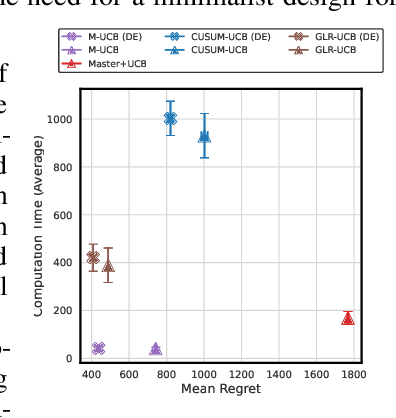
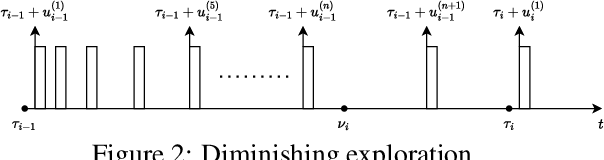
The piecewise-stationary bandit problem is an important variant of the multi-armed bandit problem that further considers abrupt changes in the reward distributions. The main theme of the problem is the trade-off between exploration for detecting environment changes and exploitation of traditional bandit algorithms. While this problem has been extensively investigated, existing works either assume knowledge about the number of change points $M$ or require extremely high computational complexity. In this work, we revisit the piecewise-stationary bandit problem from a minimalist perspective. We propose a novel and generic exploration mechanism, called diminishing exploration, which eliminates the need for knowledge about $M$ and can be used in conjunction with an existing change detection-based algorithm to achieve near-optimal regret scaling. Simulation results show that despite oblivious of $M$, equipping existing algorithms with the proposed diminishing exploration generally achieves better empirical regret than the traditional uniform exploration.