Diminishing Exploration: A Minimalist Approach to Piecewise Stationary Multi-Armed Bandits
Paper and Code
Oct 08, 2024
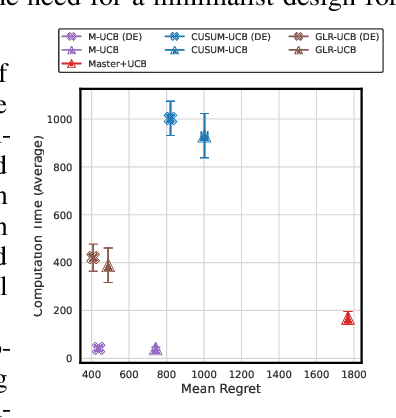
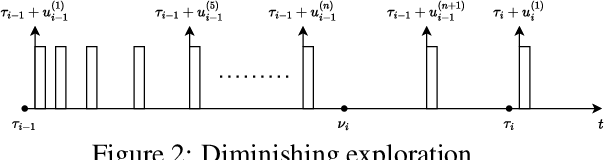

The piecewise-stationary bandit problem is an important variant of the multi-armed bandit problem that further considers abrupt changes in the reward distributions. The main theme of the problem is the trade-off between exploration for detecting environment changes and exploitation of traditional bandit algorithms. While this problem has been extensively investigated, existing works either assume knowledge about the number of change points $M$ or require extremely high computational complexity. In this work, we revisit the piecewise-stationary bandit problem from a minimalist perspective. We propose a novel and generic exploration mechanism, called diminishing exploration, which eliminates the need for knowledge about $M$ and can be used in conjunction with an existing change detection-based algorithm to achieve near-optimal regret scaling. Simulation results show that despite oblivious of $M$, equipping existing algorithms with the proposed diminishing exploration generally achieves better empirical regret than the traditional uniform exploration.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge