Polynomial-Time Algorithm for Thiele Voting Rules with Voter Interval Preferences

We present a polynomial-time algorithm for computing an optimal committee of size $k$ under any given Thiele voting rule for elections on the Voter Interval domain (i.e., when voters can be ordered so that each candidate is approved by a consecutive voters). Our result extends to the Generalized Thiele rule, in which each voter has an individual weight (scoring) sequence. This resolves a 10-year-old open problem that was originally posed for Proportional Approval Voting and later extended to every Thiele rule (Elkind and Lackner, IJCAI 2015; Peters, AAAI 2018). Our main technical ingredient is a new structural result -- a concavity theorem for families of intervals. It shows that, given two solutions of different sizes, one can construct a solution of any intermediate size whose score is at least the corresponding linear interpolation of the two scores. As a consequence, on Voter Interval profiles, the optimal total Thiele score is a concave function of the committee size. We exploit this concavity within an optimization framework based on a Lagrangian relaxation of a natural integer linear program formulation, obtained by moving the cardinality constraint into the objective. On Voter Interval profiles, the resulting constraint matrix is totally unimodular, so it can be solved in polynomial time. Our main algorithm and its proof were obtained via human--AI collaboration. In particular, a slightly simplified version of the main structural theorem used by the algorithm was obtained in a single call to Gemini Deep Think.

Outer Diversity of Structured Domains

An ordinal preference domain is a subset of preference orders that the voters are allowed to cast in an election. We introduce and study the notion of outer diversity of a domain and evaluate its value for a number of well-known structured domains, such as the single-peaked, single-crossing, group-separable, and Euclidean ones.

Diversity of Structured Domains via k-Kemeny Scores

In the k-Kemeny problem, we are given an ordinal election, i.e., a collection of votes ranking the candidates from best to worst, and we seek the smallest number of swaps of adjacent candidates that ensure that the election has at most k different rankings. We study this problem for a number of structured domains, including the single-peaked, single-crossing, group-separable, and Euclidean ones. We obtain two kinds of results: (1) We show that k-Kemeny remains intractable under most of these domains, even for k=2, and (2) we use k-Kemeny to rank these domains in terms of their diversity.

Fine-Grained Complexity and Algorithms for the Schulze Voting Method

We study computational aspects of a well-known single-winner voting rule called the Schulze method [Schulze, 2003] which is used broadly in practice. In this method the voters give (weak) ordinal preference ballots which are used to define the weighted majority graph (WMG) of direct comparisons between pairs of candidates. The choice of the winner comes from indirect comparisons in the graph, and more specifically from considering directed paths instead of direct comparisons between candidates. When the input is the WMG, to our knowledge, the fastest algorithm for computing all possible winners in the Schulze method uses a folklore reduction to the All-Pairs Bottleneck Paths (APBP) problem and runs in $O(m^{2.69})$ time, where $m$ is the number of candidates. It is an interesting open question whether this can be improved. Our first result is a combinatorial algorithm with a nearly quadratic running time for computing all possible winners. If the input to the possible winners problem is not the WMG but the preference profile, then constructing the WMG is a bottleneck that increases the running time significantly; in the special case when there are $O(m)$ voters and candidates, the running time becomes $O(m^{2.69})$, or $O(m^{2.5})$ if there is a nearly-linear time algorithm for multiplying dense square matrices. To address this bottleneck, we prove a formal equivalence between the well-studied Dominance Product problem and the problem of computing the WMG. We prove a similar connection between the so called Dominating Pairs problem and the problem of verifying whether a given candidate is a possible winner. Our paper is the first to bring fine-grained complexity into the field of computational social choice. Using it we can identify voting protocols that are unlikely to be practical for large numbers of candidates and/or voters, as their complexity is likely, say at least cubic.

Participatory Budgeting with Project Groups

We study a generalization of the standard approval-based model of participatory budgeting (PB), in which voters are providing approval ballots over a set of predefined projects and -- in addition to a global budget limit, there are several groupings of the projects, each group with its own budget limit. We study the computational complexity of identifying project bundles that maximize voter satisfaction while respecting all budget limits. We show that the problem is generally intractable and describe efficient exact algorithms for several special cases, including instances with only few groups and instances where the group structure is close to be hierarchical, as well as efficient approximation algorithms. Our results could allow, e.g., municipalities to hold richer PB processes that are thematically and geographically inclusive.

Approximation and Parameterized Complexity of Minimax Approval Voting

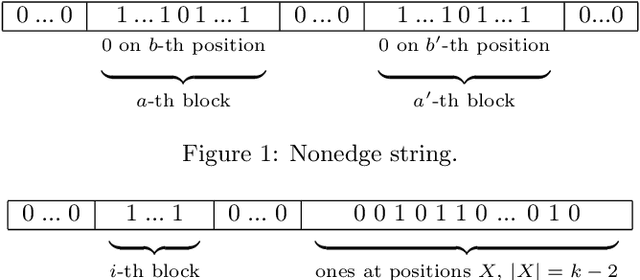
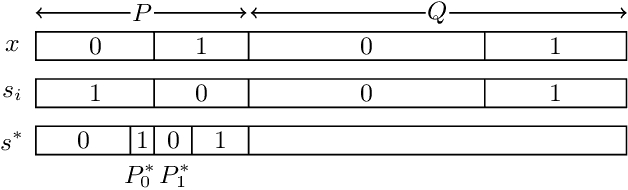
We present three results on the complexity of Minimax Approval Voting. First, we study Minimax Approval Voting parameterized by the Hamming distance $d$ from the solution to the votes. We show Minimax Approval Voting admits no algorithm running in time $\mathcal{O}^\star(2^{o(d\log d)})$, unless the Exponential Time Hypothesis (ETH) fails. This means that the $\mathcal{O}^\star(d^{2d})$ algorithm of Misra et al. [AAMAS 2015] is essentially optimal. Motivated by this, we then show a parameterized approximation scheme, running in time $\mathcal{O}^\star(\left({3}/{\epsilon}\right)^{2d})$, which is essentially tight assuming ETH. Finally, we get a new polynomial-time randomized approximation scheme for Minimax Approval Voting, which runs in time $n^{\mathcal{O}(1/\epsilon^2 \cdot \log(1/\epsilon))} \cdot \mathrm{poly}(m)$, almost matching the running time of the fastest known PTAS for Closest String due to Ma and Sun [SIAM J. Comp. 2009].