Joint Machine-Transporter Scheduling for Multistage Jobs with Adjustable Computation Time

This paper presents a scalable solution with adjustable computation time for the joint problem of scheduling and assigning machines and transporters for missions that must be completed in a fixed order of operations across multiple stages. A battery-operated multi-robot system with a maximum travel range is employed as the transporter between stages and charging them is considered as an operation. Robots are assigned to a single job until its completion. Additionally, The operation completion time is assumed to be dependent on the machine and the type of operation, but independent of the job. This work aims to minimize a weighted multi-objective goal that includes both the required time and energy consumed by the transporters. This problem is a variation of the flexible flow shop with transports, that is proven to be NP-complete. To provide a solution, time is discretized, the solution space is divided temporally, and jobs are clustered into diverse groups. Finally, an integer linear programming solver is applied within a sliding time window to determine assignments and create a schedule that minimizes the objective. The computation time can be reduced depending on the number of jobs selected at each segment, with a trade-off on optimality. The proposed algorithm finds its application in a water sampling project, where water sampling jobs are assigned to robots, sample deliveries at laboratories are scheduled, and the robots are routed to charging stations.

A Complete Set of Connectivity-aware Local Topology Manipulation Operations for Robot Swarms

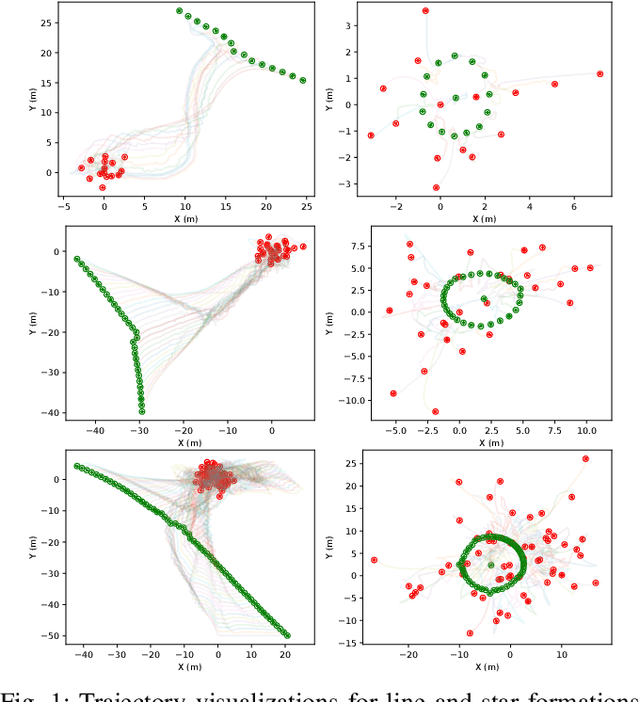
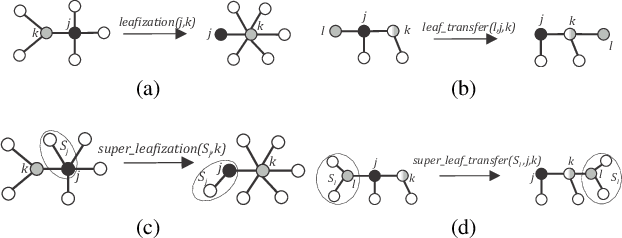
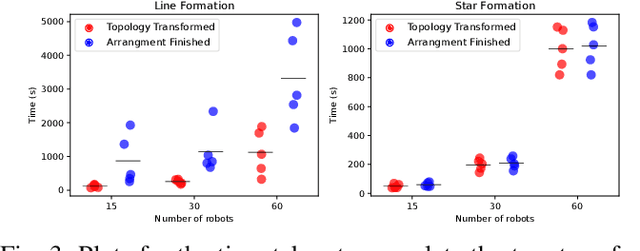
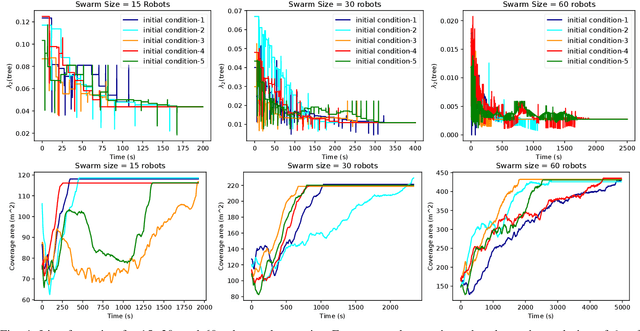
The topology of a robotic swarm affects the convergence speed of consensus and the mobility of the robots. In this paper, we prove the existence of a complete set of local topology manipulation operations that allow the transformation of a swarm topology. The set is complete in the sense that any other possible set of manipulation operations can be performed by a sequence of operations from our set. The operations are local as they depend only on the first and second hop neighbors' information to transform any initial spanning tree of the network's graph to any other connected tree with the same number of nodes. The flexibility provided by our method is similar to global methods that require full knowledge of the swarm network. We prove the existence of a sequence of transformations for any tree-to-tree transformation, and derive sequences of operations to form a line or star from any initial spanning tree. Our work provides a theoretical and practical framework for topological control of a swarm, establishing global properties using only local information.