Landscape of AI safety concerns -- A methodology to support safety assurance for AI-based autonomous systems

Artificial Intelligence (AI) has emerged as a key technology, driving advancements across a range of applications. Its integration into modern autonomous systems requires assuring safety. However, the challenge of assuring safety in systems that incorporate AI components is substantial. The lack of concrete specifications, and also the complexity of both the operational environment and the system itself, leads to various aspects of uncertain behavior and complicates the derivation of convincing evidence for system safety. Nonetheless, scholars proposed to thoroughly analyze and mitigate AI-specific insufficiencies, so-called AI safety concerns, which yields essential evidence supporting a convincing assurance case. In this paper, we build upon this idea and propose the so-called Landscape of AI Safety Concerns, a novel methodology designed to support the creation of safety assurance cases for AI-based systems by systematically demonstrating the absence of AI safety concerns. The methodology's application is illustrated through a case study involving a driverless regional train, demonstrating its practicality and effectiveness.

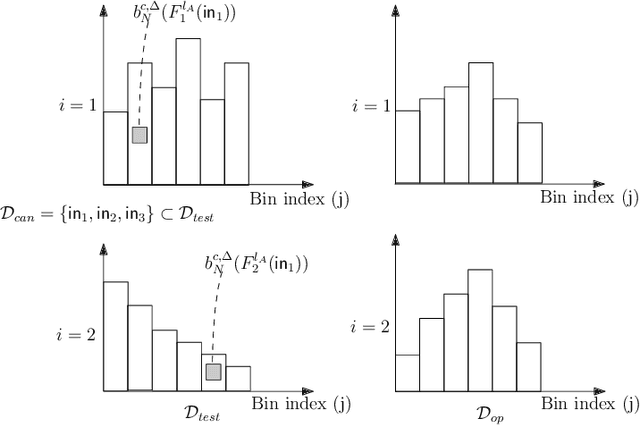
Safety Performance of Neural Networks in the Presence of Covariate Shift

Covariate shift may impact the operational safety performance of neural networks. A re-evaluation of the safety performance, however, requires collecting new operational data and creating corresponding ground truth labels, which often is not possible during operation. We are therefore proposing to reshape the initial test set, as used for the safety performance evaluation prior to deployment, based on an approximation of the operational data. This approximation is obtained by observing and learning the distribution of activation patterns of neurons in the network during operation. The reshaped test set reflects the distribution of neuron activation values as observed during operation, and may therefore be used for re-evaluating safety performance in the presence of covariate shift. First, we derive conservative bounds on the values of neurons by applying finite binning and static dataflow analysis. Second, we formulate a mixed integer linear programming (MILP) constraint for constructing the minimum set of data points to be removed in the test set, such that the difference between the discretized test and operational distributions is bounded. We discuss potential benefits and limitations of this constraint-based approach based on our initial experience with an implemented research prototype.